Derivation of Refractive Index of Prism

Watch the video lecture to learn how to find out the Refractive Index of Prism

Click the link to watch the video lecture

Circles

Triangle Multiple choice questions based Online Test

Useful for competitive aspirants and schooling students of class 10. 

To participate into the test open the link below

👇

Circles

To watch the video lecture open the link below

👇

Theorem 10.1

Triangle

Triangle Multiple choice questions based Online Test

Useful for competitive aspirants and schooling students of class 10. 

To participate into the test open the link below

👇

Triangle Multiple Choice Questions Based Test

Thales Theorem

Statement and prove.

Watch the video lecture

To watch click the link below

👇

Theles Theorem

Theorem 6.2

Useful for Schooling students/Competitive Aspirants

To watch click the link below 

👇

Theorem 6.2 Video Lecture

काल परीक्षा (Clock And Calendar Test)

काल परीक्षा (Clock And Calendar Test) शार्ट ट्रिक और उदहारण

काल परीक्षण में आपसे कैलेण्डर, घड़ी और समय संबंधी प्रश्न पूछे जाते हैं। इसके लिए आपको कैलेण्डर, घड़ी और समय का ज्ञान पूर्णतः होना चाहिए। कुछ आवश्यक जानकारियाँ निम्नलिखित हैं:

• सप्ताह में सात दिन होते हैं – रविवार, सोमवार, मंगलवार, बुधवार, बृहस्पतिवार, शुक्रवार तथा शनिवार।
• एक वर्ष में बारह महीने होते हैं – जनवरी (31 दिन), फरवरी (28 या 29 दिन), मार्च (31 दिन), अप्रैल (30 दिन), मई (31 दिन), जून (30 दिन), जुलाई (31 दिन), अगस्त (31 दिन), सितम्बर (30 दिन), अक्टूबर (31 दिन), नवम्बर (30 दिन), दिसम्बर (31 दिन)।
• यदि कोई वर्ष 4 से पूर्णतः विभाजित हो जाता है, तो वह वर्ष ‘लीप वर्ष’ कहलाता है।
• साधारणतः फरवरी 28 दिन का होता है, परन्तु लीप वर्ष में फरवरी 29 दिन का होता है।
• एक वर्ष में 52 सप्ताह तथा एक दिन होते हैं तथा लीप वर्ष में 52 सप्ताह तथा दो दिन होते हैं।
• दिनों की संख्या को सात से भाग देने पर जो शेष बचता है, उसे विषम दिन कहते हैं।
• एक दिन या वार की पुनरावृत्ति प्रत्येक 7, 14, 21, 28, … 364 दिनों के बाद होती है।
• घड़ी की सूइयाँ जब अपने वृत्ताकार मार्ग पर एक पूर्ण चक्कर लगाती है, तब उन्हें 360° घूमना पड़ता है।
• एक मिनट की दूरी 6° के बराबर होता है।
• जब मिनट की सूई एक मिनट की दूरी तय करती है, तो घण्टे की सूई 1/2° के बराबर आगे बढ़ जाती है।
• एक घण्टा में 60 मिनट तथा 1 मिनट में 60 सेकण्ड होते हैं।
• प्रत्येक एक घण्टे में मिनट की सूई घण्टे की सूई से 55 मिनट दूरी आगे बढ़ जाती है।
• प्रत्येक घण्टे में दोनों सूइयाँ एक ही दिशा में एक बार मिलती हैं, लेकिन 12 घण्टें में 11 बार तथा 24 घण्टे में 22 बार मिलती हैं।
• प्रत्येक घण्टे में दोनों सूइयाँ केवल एक बार विपरीत दिशा में होती हैं, लेकिन 12 घण्टे में 11 बार तथा 24 घण्टे में 22 विपरीत होती हैं।
• प्रत्येक घण्टे में दोनों सूइयाँ दो बार समकोण बनाती हैं, लेकिन 12 घण्टे में 24 बार परस्पर समकोण बनाती हैं।
• प्रत्येक घण्टे में दोनों सूइयाँ दो बार समकोण बनाती हैं तथा इस दशा में दोनों सूइयों के बीच की दूरी 15 मिनट के बराबर होती है।

पूछे जाने वाले प्रश्नों पर एक दृष्टि

उदाहरण 1. यदि किसी महीने की तीसरी तारीख को मंगलवार है, तो उसी महीने की 27 तारीख से चार दिन पहले कौन-सा दिन होगा?

1. मंगलवार
2. सोमवार
3. बुधवार
4. रविवार

हल (2): 27 – 3 = 24

विषम दिनों की कुल संख्या = 3

मंगलवार + 3 ⇒ शुक्रवार – 4 ⇒ सोमवार

उदाहरण 2. प्रकाश को याद है कि उसके पिताजी का जन्मदिन 13 और 16 अप्रैल के बीच किसी दिन है, जबकि उसकी बहन को याद है कि उसके पिताजी का जन्म-दिन 14 अप्रैल के बाद लेकिन 17 अप्रैल के पहले किसी दिन है। बताएँ कि इनके पिताजी का जन्म दिन किस दिन को है?

1. 14 अप्रैल
2. 15 या 16 अप्रैल
3. 14 या 15 अप्रैल
4. 15 अप्रैल

हल (4):

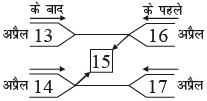
अतः, अभीष्ट तिथि ⇒ 15 अप्रैल।

चूँकि दोनों कथनानुसार 13 और 14 के बाद एवं 16 तथा 17 के पहले वो तिथि है। अर्थात् 13, 14, 16 एवं 17 ये तिथियाँ अमान्य हो जाएँगी। इसलिए अब हम देखेंगे कि 14 एवं 16 के बीच कौन सी तिथि है। हम जानते हैं कि 14 एवं 16 के बीच में केवल 15 एक तिथि है तथा दोनों कथनों में भी केवल 15 ही एक ऐसी तिथि है जो कि उभयनिष्ठ है।

सूक्ष्म विधि

अभीष्ट तिथि = दोनों तिथियों में, ‘के बाद’ में प्रयुक्त तिथियों में से बड़ी तिथि + 1

= 14 + 1 ⇒ 15 या

अभीष्ट तिथि = दोनों तिथियों में, ‘के पहले’ प्रयुक्त तिथियों में से छोटी तिथि – 1

= 16 – 1 ⇒ 15

अतः प्रकाश के पिताजी का जन्म-दिन 15 अप्रैल को है।

उदाहरण 3. प्रशिक्षक महोदय 8:35 बजे खेल के मैदान में पहुँचे। राजेश 45 मिनट देर से पहुँचा और इस प्रकार वह प्रशिक्षण के समय से 15 मिनट देर था। बताएँ कि प्रशिक्षक महोदय निर्धारित समय से कितने मिनट पहले पहुँचे थे?

1. 15 मिनट
2. 30 मिनट
3. 45 मिनट
4. 25 मिनट

हल (2): प्रशिक्षक महोदय के पहुँचने का समय → 8:35

राकेश 45 मिनट देर से पहुँचा → +45 मिनट

∴ राकेश के पहुँचने का समय = 9:20

राकेश प्रशिक्षण के निर्धारित समय से देर → -15 मिनट

∴ प्रशिक्षण का निर्धारित समय = 9:05

चूँकि प्रशिक्षण का निर्धारण समय 9:05 है, और प्रशिक्षक महोदय 8:35 में ही पहुँच गये थे।

अतः वे प्रशिक्षण के निर्धारित समय से (9:05 – 8:35 ⇒ 30) 30 मिनट पहले पहुँचे थे।

चूँकि प्रशिक्षक महोदय 8:35 बजे पहुँचे हैं और राकेश उनसे 45 मिनट देर से पहुँचा यानी राकेश (8:35 + 45 = 9:20) 9:20 बजे पहुँचा फिर भी वह प्रशिक्षण के निर्धारित समय से 15 मिनट विलम्ब था, यानी प्रशिक्षण का निर्धारित समय (9:20 – 15 = 9:05 =) 9:05 बजे है। चूँकि प्रशिक्षक महोदय के पहुँचने का समय 8:35 बजे है। अतः प्रशिक्षक महोदय निर्धारित समय (9:05 – 8:35 = 30) से 30 मिनट पहले पहुँचे थे।

सूक्ष्म विधि

8:35 + 30 – 8:35 ⇒ 30 मिनट या

45 – 15 ⇒ 30 मिनट

साधित उदाहरण (Solved Examples)

1. इस वर्ष बालू का जन्मदिन 27 जनवरी अर्थात् बुधवार को पड़ता है। बालू को याद है कि मोहन का जन्मदिन उसके जन्मदिन के बाद ठीक पांचवे शुक्रवार को पड़ता है। मोहन बालू से कितना छोटा है?

1. आंकडे अधूरे हैं
2. 30 दिन
3. 31 दिन
4. 29 दिन

हल (2): बुधवार के दो दिन बाद पहला शुक्रवार होगा। दिनों की कुल संख्या

= 2 + (7 × 4) = 30 दिन

2. शैलेश ने सोमवार को फिल्म देखी। नितिन ने विकास से दो दिन पहले किंतु शैलेश से तीन दिन बाद फिल्म देखी। विकास ने किस दिन फिल्म देखी?

1. सोमवार
2. शनिवार
3. मंगलवार
4. रविवार

हल (2): नितिन ने सोमवार + 3 = बृहस्पतिवार को फिल्म देखी।

विकास ने बृहस्पतिवार + 2 = शनिवार को फिल्म देखी।

Clock And Calendar Test -

Clock And Calendar Test - Short-cut Tricks And Examples

The clock has 12 hours numbered from 1 to 12. Also, the clock is divided into 60 equal minute divisions. Therefore, each hour number is separated by five minute divisions.

If a watch or a clock indicates 8.15, when the correct time is 8, it is said to be 15 minutes too fast. On the other hand, if it indicates 7.45, when the correct time is 8, it is said to be 15 minutes too slow.

Minute Spaces

The face or dial of watch is a circle whose circumference is divided into 60 equal parts, called minute spaces.

Hour Hand and Minute Hand

A clock has two hands, the smaller one is called the hour hand or short hand while the larger one is called minute hand or long hand.

Relative position of the hands

The position of the M.H. relative to the H.H. is said to be the same, whenever the M.H. is separated from the H.H. by the same number of minute divisions and is on same side (clockwise or anticlockwise) of the H.H. Any relative position of the hands of a clock is repeated 11 times in every 12 hours.

1. When both hands are 15 minute spaces apart, they are at right angle.
2. When they are 30 minute spaces apart, they point in opposite directions.
3. The hands are in the same straight line when they are coincident or opposite to each other.

Incorrect Clock

If a clock indicates 6 : 10, when the correct time is 6 : 00, it is said to be 10 minute to fast and if it indicates 5 : 50 when the correct time is 6 : 00, it is said to be 10 minute slow.

If both hands coincide at an interval x minutes and 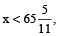 then total time gainedand clock is said to be ‘fast’.

If both hands coincide at an interval x minutes and 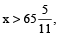then total time lost and clock is said to be ‘slow’.

Points to Remember

One minute division =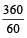= 6° apart. i.e. In one minute, the minute hand moves 6°.

One hour division = 6° × 5 = 30° apart. i.e. In one hour, the hour hand moves 30° apart.

Also, in one minute, the hour hand moves = 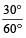= 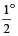apart.

Since, in one minute, minute hand moves 6° and hour hand moves 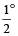, therefore, in one minute, the minute hand gains  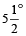more than hour hand.

In one hour, the minute hand gains 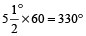over the hour hand. i.e. the minute hand gains 55 minutes divisions over the hour hand.

In every hour, both the hand coincide once.

In a day, the hands are coinciding 22 times.

In every 12 hours, the hands of clock coincide 11 times.

In every 12 hours, the hands of clock are in opposite direction 11 times.

In every 12 hours, the hands of clock are at right angles 22 times.

In every hour, the two hands are at right angles 2 times.

In every hour, the two hands are in opposite direction once.

In a day, the two hands are at right angles 44 times.

If both the hands coincide, then they will again coincide after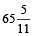minutes. i.e. in correct clock, both hand coincide at an interval of  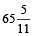minutes.

If the two hands coincide in time less than 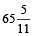 minutes, then clock is too fast and if the two hands coincides in time more than  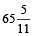minutes, then the clock is too slow.

Solved Examples

Question 1. Find the angle between the minute hand and hour hand of a clock when the time is 7.20

Solution: Angle traced by hour hand in 12 hours = 360 Degrees

Angle traced by it in 7 hrs 20 min i.e 22/3 hrs

= (360/12) × (22/3)= 2200

Angle traced by minute hand in 60 min = 3600

Angle traced by it in 20 minutes = (360/60) × 20 = 1200

Required angle = (2200 – 1200) = 1000

Question 2. At what time between 2 and 3 o’ clock will the hands of a clock together ?

Solution: At 2 o’ clock, the hour hand is at 2 and minute hand at 12, i.e., they are 10 minute spaces apart.

To be together , the minute hand must gain 10 minutes over the hour hand.

Now, 55 minutes are gaines by it in 60 minutes

10 minutes will be gained in {(60/55) × 10} min =10 10/11 min

The hands will coincide at 10 10/11 min past 2

Question 3. At what time between 4 and 5 o’ clock will the hands of a clock be at right angle ?

Solution: At 4 o’ clock, the minute hand will be 20 min spaces behind the hour hand.

Now , when the two hands are at right angles, they are 15 min. spaces apart.

So, they are at right angles in following two cases

Case I: When minute hand is 15 minute spaces behind the hour hand

In this case min hand will have to gain (20 –15) = 5 minute spaces

55 min. spaces will be gained by it in (60 × 5)/55 min = 5 5/11 min

They are at right angles at 5 5/1 min past 4

Case II: When the minute hand is 15 minute spaces ahead of the hour hand

They are at right angles at 38 2/11 min past 4

Question 4. At what time between 4 and 5 will the hands of a watch

(i) coincide, and (ii) point in opposite directions.

Solution:

(i) At 4 O’ clock, the hands are 20 minutes apart. Clearly the minute hand must gain 20 minutes before two hands can be coincident.

But the minute-hand gains 55 minutes in 60 minutes.

Let minute hand will gain x minute in 20 minutes.

So,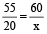 

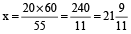⇒  min.

∴ The hands will be together at 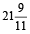 min past 4.

(ii) Hands will be opposite to each other when there is a space of 30 minutes between them. This will happen when the minute hand gains (20 + 30) = 50 minutes.

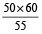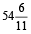Now, the minute hand gains 50 min in  or  min.

∴  The hands are opposite to each other at 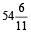 min past 4.

Question 5. What is the angle between the hour hand and minute hand when it was 5 : 05 pm.

Solution: 5.05 pm means hour hand was on 5 and minute hand was on 1, i.e. there will be 20 minutes gap.

∴  Angle = 20 × 6° = 120° [1 minute = 6°]

Question 6. My watch, which gains uniformly, is 2 min slow at noon on Sunday, and is 4 minutes 48 seconds fast at 2 pm on the following Sunday. When was it correct ?

Solution: From Sunday noon to the following Sunday at 2 pm

= 7 days 2 hours = 170 hours.

The watch gains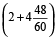=  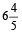minutes in 170 hours.

∴  The watch gains 2 minutes in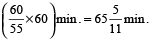 

Now, 50 hours = 2 days 2 hours.

2 days 2 hours from Sunday noon = 2 pm on Tuesday.

Question 7. The minute hand of a clock overtakes the hour hand at intervals of 65 minutes of the correct time. How much a day does the clock gain or lose?

Solution: In a correct clock, the minute hand gains 55 min. spaces over the hour hand in 60 minutes.

To be together again, the minute hand must gain 60 minutes over the hour hand.

55 min. are gained in 

But, they are together after 65 min.

∴  Gain in 65 min. 

Gain in 24 hours 

∴  The clock gains  minutes in 24 hours.

Question 8. A man who went out between 5 or 6 and returned between 6 and 7 found that the hands of the watch had exactly changed place. When did he go out?

Solution: Between 5 and 6 to 6 and 7, hands will change place after crossing each other one time. i.e., they together will make 1 + 1 = 2 complete revolutions.

H.H. will move through

 or  minute divisions.

Between 5 and 6 → minute divisions.

At 5, minute hand is 25 minute divisions behind the hour-hand.

Hence it will have to gain  minute divisions on the hour-hand

 minute divisions on the hour hand.

The minute hand gains minute divisions

 minutes  minutes

∴ The required time of departure is min past 5.

Calendar

The Julian calendar is a reform of the Roman calendar introduced by Julius Caesar in 46 BC (708 AUC). It took effect the following year, 45 BC (709 AUC), and continued to be used as the civil calendar in some countries into the 20th century. The calendar has a regular year of 365 days divided into 12 months, as listed in Table of months. A leap day is added to February every four years. The Julian year is, therefore, on average 365.25 days long.

The calendar year was intended to approximate the tropical (solar) year. Although Greek astronomers had known, at least since Hipparchus, that the tropical year was a few minutes shorter than 365.25 days, the calendar did not compensate for this difference. As a result, the calendar year gained about three days every four centuries compared to observed equinox times and the seasons. This discrepancy was corrected by the Gregorian reform, introduced in 1582.

The Julian calendar has been replaced by the Gregorian calendar in all countries which formerly used it as the civil calendar. Most Christian denominations have also replaced it with the Gregorian calendar as the basis for their liturgical calendars.

Points to Remember

Odd Days
We are supposed to find the day of the week on a given date. For this, we use the concept of ‘odd days’.In a given period, the number of days more than the complete weeks are called odd days.
Leap Year

• Every year divisible by 4 is a leap year, if it is not a century.
• Every 4th century is a leap year and no other century is a leap year.

Note: A leap year has 366 days.

Examples:

• Each of the years 1948, 2004, 1676 etc. is a leap year.
• Each of the years 400, 800, 1200, 1600, 2000 etc. is a leap year.
• None of the years 2001, 2002, 2003, 2005, 1800, 2100 is a leap year.

Ordinary Year

The year which is not a leap year is called an ordinary years. An ordinary year has 365 days.

Counting of Odd Days

• 1 ordinary year = 365 days = (52 weeks + 1 day.)
• 1 ordinary year has 1 odd day.
• 1 leap year = 366 days = (52 weeks + 2 days)
• 1 leap year has 2 odd days.
• 100 years = 76 ordinary years + 24 leap years = (76 × 1 + 24 × 2) odd days = 124 odd days. = (17 weeks + 5 days) = 5 odd days.
• Number of odd days in 100 years = 5.
• Number of odd days in 200 years = (5 × 2)→ 3 odd days.
• Number of odd days in 300 years = (5 × 3) → 1 odd day.
• Number of odd days in 400 years = (5 × 4 + 1)→ 0 odd day.
• Similarly, each one of 800 years, 1200 years, 1600 years, 2000 years etc. has 0 odd days.

Day of the Week Related to Odd Days:

No. of days:	0	1	2	3	4	5	6
Day:	Sun.	Mon.	Tues.	Wed.	Thurs.	Fri.	Sat.

Solved Examples

Question 1. What day of the week was 15th August 1949?

Solution: 15th August 1949 means

1948 complete years + first 7 months of the year 1949 + 15 days of August.

1600 years give no odd days.

300 years give 1 odd day.

48 years give {48 + 12} = 60 = 4 odd days.

[For ordinary years → 48 odd days and for leap year 1 more day (48 ÷ 4) = 12 odd days;

60 = 7 × 8 + 4]

From 1st January to 15th August 1949

Odd days : January – 3; February – 0; March – 3; April – 2; May – 3; June – 2; July – 3; August – 1

17 ⇒ 3 odd days.

∴ 15th August 1949 → 1 + 4 + 3 = 8 = 1 odd day.

This means that 15th Aug. fell on 1st day.

Therefore, the required day was Monday.

Question 2. How many times does the 29th day of the month occur in 400 consecutive years?

Solution: In 400 consecutive years, there are 97 leap years.

Hence, in 400 consecutive years, February has the 29th day 97 times and the remaining eleven months have the 29th day
400 × 11 = 4400 times

∴ The 29th day of the month occurs

(4400 + 97) or 4497 times.

Question 3. Today is 5th February. The day of the week is Tuesday. This is a leap year. What will be the day of the week on this date after 5 years?

Solution: This is a leap year. So, next 3 years will give one odd day each. then leap year gives 2 odd days and then again next year give 1 odd day.

Therefore (3 + 2 + 1) = 6 odd days will be there.

Hence the day of the week will be 6 odd days beyond Tuesday, i.e., it will be Monday.

Question 4. What day of the week was 20th June 1837?

Solution: 20th June 1837 means 1836 complete years

+ first 5 months of the year 1837 + 20 days of June.

1600 years give no odd days.

200 years give 3 odd days.

36 years give (36 + 9) or 3 odd days.

1836 years give 6 odd days.

From 1st January to 20th June there are 3 odd days.

Odd days : January — 3; February — 0; March — 3; April — 2; May — 3; June — 6

Total odd days =17 ⇒ 3 odd days.

Therefore, the total number of odd days = (6 + 3) or 2 odd days.

This means that the 20th of June fell on the 2nd day commencing from Monday.

Therefore, the required day was Tuesday.

Question 5. Prove that the calender for 1990 will same for 2001 also.

Solution: It is clear that the calender for 1990 will same for 2001 if first January of both the years is the same weekdays. For that the number of odd days between 31st December 1989 and 31st December 2000 must be zero. Odd days are as given below:

Year	1990	1991	1992	1993	1994	1995
Odd days	1	1	(L) 2	1	1	1
Year	1996	1997	1998	1999	2000
Odd days	(L) 2	1	1	1	(L) 2

Total number of odd days = 14 ⇒ 0 odd days.

 

 

Rankings and Time Sequence

Ranking And Time Sequence - Short-cut Tricks And Examples

Dear Reader, below are five simple types of ‘ranking and time sequence’ problems. You will find detailed solutions with each of the problems

As far as ranking problems are concerned, you have to remember one simple formula.

Total number of people = Rank of a person from START + Rank of person from the END – 1

Let we start with our tutorial. At the end of the tutorial, you will find a short practice test. Please do take the test so that you can be double sure that you have understood well.

Type I: Finding Rank From the Start (or the End)

In type 1, you will know the rank of a person from either the start (or the end). Using that data, you have to find the rank of that person from the end (or the start). Below example will help you.

Example Question 1: Reena is 10 ranks ahead of Priya in a class of 40. If Priya`s rank is 20th from the last, what is Reena`s rank from the start?
Answer: 31th

Solution:
Priya’s rank from the last is 20. Reena is 10 ranks ahead. Therefore, Reena’s rank from the last = Rank of Reena from the last = 20 – 10 = 10th
Now you have to apply the formula that you saw in the introduction.
Total number of students = Rank of Reena from the start + Rank of Reena from the end – 1
40 = Rank of Reena from the start + 10 – 1
Rank of Reena from the start = (40 – 10) +1
= 31th

Type II: Finding Total Number of People in a Sequence

In type 2, you will find ranks of a person from the start and the end. You have to find the total number of people. Let us see an example.

Example Question 2: Venkatesh ranks 8th from the top and 24th from the bottom in the class. How many students are there in total?
Answer: 31

Solution:
Total number of Students = Rank of Venkatesh from the top + Rank of Venkatesh from the bottom – 1
= [8 + 24] – 1= 31

Type III: Interchanging Positions

In this type, positions of the people in a sequence will be interchanged. You have to solve these problems after processing the data given.

Example Question 3: In a row of girls, Uma is 10th from the left and Meena is 20th from the right. If they interchange their positions, Uma becomes 15th from the left. How many girls are there in the row?
Answer: 34

Solution:
After interchange, rank of Uma from the left = 15
But, before interchange, Meena was 20th from the right. After interchange, Uma would have occupied the same position of Meena’s earlier spot. Therefore,
Present rank of Uma from the right = 20
Now you know the current ranks of Uma from left as well as right. Therefore,
Total number of girls = Uma’s rank from the left + Uma’s rank from the right – 1
= (15+20)-1
=34.

Type IV: Intervention in a Frequent Event

Though the heading of this type looks complicated, this is one of the easiest. There will be intervention at certain time of a frequent event. Based on that time data you have to solve the problem logically.

Let us see an example.

Example Question 4: A bus leaves to Chennai from Bangalore every 30 minutes. A passenger inquired about the next bus to Bangalore, and he was informed that the bus left 15 minutes before, and the next bus will be at 5.00 pm. Find at what time the passenger had enquired?
Answer: 4.45 pm

Solution:
For every 30 minutes, there is a bus. The next bus will be at 5.00 pm, so the last bus must have left at 4.30 pm.
The informer said that the bus had left 15 minutes before his inquiry. So the time of inquiry is 4.30 + 0.15 = 4.45 pm.

Type V: Day of Week Based on Frequency

This type is very easy just like the previous one. You can answer this with little effort. (You may not expect questions simple in your exam. However, this will be a first step in understanding more difficult questions.)

Example Question 5: Gita went to the temple five days ago. If she goes to the temple every Friday, then what day of the week is today?
Answer: Wednesday

Solution:
She went to temple five days ago i.e., Friday.
Five days from Friday is Wednesday.

Venn Diagram Test

Venn Diagram Test - Short-cut Tricks And Examples

Type 1: Matching the Relationship

You will find a set of things in the question. You have to find the best diagram that fits the connection between the things. Below is an example to help you.

Example Question 1: Which of the following diagram indicates the best relation between Pen, Nib and Pencil?

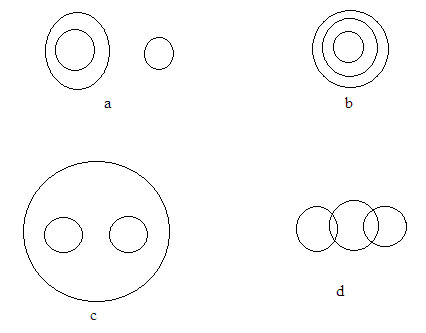
Answer: a
Reason:
The relation between pen, nib and pencil.
Nib is a component or part of pen and pencil is different from both.
Among the options, option a represents one circle inside the other i.e. nib is the part of pen and another circle individually which represent pencil that does not have relation with other two.

Type 2: Numbers (Data) Inside Diagram

In this type, you will find numbers (data) in Venn diagrams. You have to find the answers based on the data.

Below is an example question.

Example Question 2: In the below diagram, rectangle represents Dancer, triangle represents Singer and circle represents Dramatist.

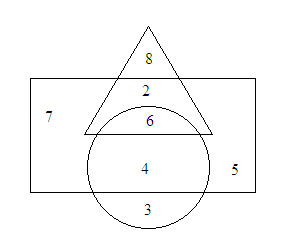
1. How many dancers are also singers?
a) 7 b) 5 c) 8 d) 2
Answer: c) 8
Reason:
Rectangle represents dancers. Triangle represents singers. To find the dancers who are also singers, see the overlap area between rectangle and triangle.
The overlap contains 6 and 2. Therefore, the answer is 6+2 = 8.

2. How many dramatist are both dancers and singers?
a) 6 b) 5 c) 8 d) 2
Answer: a) 6

3. how many singers are neither dancers nor dramatist?
a) 6 b) 4 c) 8 d) 2
Answer: a) 8
Reason:
You have to find the area that represents only singers and neither dancer nor dramatists. Therefore, you observe the part in triangle that is not a part of rectangle or circle.
The part of triangle separate from rectangle and circle contains 8.
Therefore, 8 is the answer.