Slope of a Line
A line in a coordinate plane forms two angles with the x-axis, which are supplementary.
The angle (say) θ made by the line l with positive direction of x-axis and measured anti clockwise is called the inclination of the line.
Obviously 0° ≤ θ ≤ 180° (Fig 9.2).
We observe that lines parallel to x-axis, or coinciding with x-axis, have inclination of 0°. The inclination of a vertical line (parallel to or coinciding with y-axis) is 90°.
Definition 1
If θ is the inclination of a line l, then tan θ is called the slope or gradient of the line l.
The slope of a line whose inclination is 90° is not defined.
The slope of a line is denoted by m. Thus, m = tan θ, θ ≠ 90°
It may be observed that the slope of x-axis is zero and slope of y-axis is not defined.
Slope of a line when co-ordinate of any two points on the line are given.
We know that a line is completely determined when we are given two points on it.Hence, we proceed to find the slope of a line in terms of the coordinates of two points on the line.
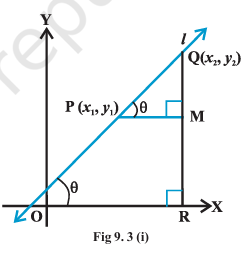
Let P(x1 , y1 ) and Q(x2 , y2 ) be two points on non-vertical line l whose inclination is θ. Obviously, x1 ≠ x2 , otherwise the line will become perpendicular to x-axis and its slope will not be defined.
The inclination of the line l may be acute or obtuse. Let us take these two cases.
Draw perpendicular QR to x-axis and
PM perpendicular to RQ as shown in
Figs. 9.3 (i) and (ii).
Case 1
When angle θ is acute:
In Fig 9.3 (i), ∠MPQ = θ ............. (i)
Therefore, slope of line l = m = tan θ. MQ But in ∆MPQ, we have
tanθ
= MQ/MP = y2 - y1/x2 - x1 ............... (ii)
m = y2 - y1/x2 - x1
Video Lecture Related to Slope of a Line when two points are given (For Acute Angle)
Case II
Video Lecture Related to Slope of a Line when two points are given (For Obtuse Angle)
When angle θ is obtuse: In Fig 9.3 (ii), we have ∠MPQ = 180° – θ.
Therefore, θ = 180° – ∠MPQ.
Now, slope of the line l
m = tan θ = tan ( 180° – ∠MPQ)
= – tan ∠MPQ = − QM/ PM =− (y2 - y1)/ (x1 - x2)
Consequently, we see that in both the cases the slope m of the line through the points
(x1, y1) and (x2,y2) is given by
m = y2 - y1/x2 - x1