कोडेड इन-इक्वलिटी (Coded Inequalities) शार्ट ट्रिक और उदहारण
अक्षरों एवं गणितीय चिह्नों या संकेतों के माध्यम से संयोजित समीकरण जो कि गणितीय नियमों के आधार पर व्यवस्थित किए गए होते हैं ऐसे ही समीकरण रूपी संयोजन को गणितीय कथन कहते हैं। जैसे –
- ‘P < Q' का अर्थ है 'P, Q से छोटा है’
- ‘P ≤ Q’ का अर्थ है ‘P, Q से या तो छोटा है या समान है’
- ‘P > Q’ का अर्थ है ‘P, Q से बडा है’
- ‘P ≥ Q’ का अर्थ है ‘P, Q से बड़ा है या समान है’
- ‘P = Q’ का अर्थ है ‘P, Q के समान है’ आदि।
दिये गये कथनों के आधार पर जो यथार्थ स्थापित किये जाते हैं उसे निष्कर्ष कहते हैं।
उदाहरणस्वरूप: A > B, C > A
निष्कर्ष
I. C > B,
II. C = B
उपर्युक्त कथनों को एक साथ समायोजित करने पर C > A > B
यहाँ हम देख रहे हैं कि C, A और B दोनों से ही बड़ा है जबकि पहले निष्कर्ष में C > B व्यक्त किया गया है जो कि कथनों के संयोजन के बिल्कुल ही अनुरूप है लेकिन दूसरे निष्कर्ष में
C = B व्यक्त किया गया है जो कि कथनों के संयोजन के अनुरूप नहीं है।
अतः दिये गये कथनों आधार पर दोनों निष्कर्षों में से केवल प्रथम निष्कर्ष तर्कसंगत है।
कथनों का गणितीय चिह्नों के साथ निरूपण
सर्वप्रथम हमें इस प्रकार के प्रश्नों को हल करने के लिये दिये गए कथन में प्रयुक्त चिह्नों को निर्देशानुसार गणितीय चिह्नों के साथ निरूपित कर लेना चाहिये।
निम्नलिखित गणितीय चिह्नों के साथ निरूपण् की प्रक्रिया पर एक नजर डालें:
निर्देश
- A @ B का आशय → ‘A, B से छोटा है।’
- A @ B का आशय → ‘A, या तो B से छोटा है या B के बराबर है।’
- A = B का आशय → ‘A, B के बराबर है।’
- A © B का आशय → ‘A, B से बड़ा है।’
- A © B का आशय → ‘A, या तो B से बड़ा है, या B के बराबर है।’
कथन: Z @ P, P © Q, Q @ N
उपर्युक्त कथन को हम निम्न प्रकार से गणितीय चिह्नों के साथ निरूपित कर कर सकते हैं
Z < P, P ≥ Q, Q ≤ N [/av_textblock][av_textblock size='' font_color='' color='' custom_class='']
कथनों के संयोजन के विशेष तथ्य:
कथनों को संयोजित करते समय दिये गए निर्देश के अतिरिक्त अपनी ओर से कोई भी कल्पना नहीं करें।
दिये गए कथन को हमें हमेशा ही घटते क्रम में संयोजित करना चाहिए। जैसे: Z < P ⇒ P > Z
घटते क्रम में संयोजित करने के बाद हमें यह प्रयास करना चाहिए कि कथन में दिये गए अधिक से अधिक खण्ड आपस में संयोजित हो जाएँ।
जैसे- P > Z, P ≥ Q, N ≥ Q
- यहाँ हम देख रहे हैं कि ‘P’ Z, और Q से तो बड़ा है लेकिन ‘P’, N से बड़ा है या छोटा है या बराबर है इसकी निश्चितता व्यक्त नहीं की जा सकती। लेकिन एक तथ्य जो और हम देख रहे हैं वह यह है कि P और N दोनों ही Q से बडे भी हैं साथ ही P और N दोनों ही Q के बराबर भी हैं।
- उपर्युक्त चरणों के बाद हमें यह प्रयास करना चाहिये कि संयोजन की अधिक से अधिक कितनी संभावनाएँ प्राप्त हो सकती हैं।
जैसे- P > Z ≥ Q, N ≥ Q

यहाँ हमें निम्न संभावनाएँ प्राप्त हो रही हैं:
(i) ‘P’ Z, से बड़ा है
(ii) ‘P’, Q से बड़ा है
(iii) ‘N’, Q से बड़ा है। या,
- ‘P’, Z, Q, और N तीनों से बड़ा है
- ‘Z’, Q और N बराबर हैं।
निष्कर्षों का गणितीय चिह्नों के साथ निरूपण:
कथन: Z @ P, P © Q, Q @ N
निष्कर्ष:
I. A @ N
II. N © P
अब हम इसे कथनों के ही संयोजन की प्रक्रिया की ही तरह घटते क्रम में एवं संभावित समीकरणों में व्यवस्थित करेंगे।
जैसे-
I. Z ≤ N ⇒ N > या N = Z
II. N > P
यहाँ दिये गए दोनों ही निष्कर्ष असत्य हैं। क्योकि कि निष्कर्ष I, ‘या तो संभावना’ (either possibility) को व्यक्त कर रहा है जिसमें संभावित स्थिति के अनुसार ‘N = Z’ कथनों के केवल एक क्रम को अनुसरण करता है पर नियमानुसार यदि कोई एक ही निष्कर्ष दो संभावनाओं को व्यक्त करता हो, तो ऐसा निष्कर्ष असत्य माना जाता है। साथ ही निष्कर्ष I में N को Z से बड़ा के रूप में (N > Z) दर्शाया गया है जबकि कथनानुसार N और Z के बीच ऐसा संबंध संभव ही नहीं है।
इसी प्रकार निष्कर्ष II भी असत्य है क्योकि कि संभावना I के तहत N और P में कोई संबंध स्थापित नहीं हो रहा है। जबकि संभावना II के आधार पर ‘P’, N से बड़ा है। लेकिन यहाँ ध्यान रहे कि यदि निष्कर्ष II में ‘P > N’ भी होता तो भी वह असत्य ही माना जाता। क्योकि कि यदि कथनों को संयोजित करने पर दो स्थितियाँ प्राप्त होती है, तो ऐसी स्थिति में कोई भी निष्कर्ष तभी सत्य होते हैं जबकि वे निष्कर्षों की सत्यता के निर्धारण के लिये व्यक्त किये गये निम्नलिखित नियम का अनुपालन करें।
निष्कर्षों की सत्यता का निर्धारण
- निष्कर्ष की सत्यता या असत्यता के लिये कथनों एवं निष्कर्षों दोनों के ही संयोजन की स्थिति पर गौर करना चाहिए।
- यदि कथनों को संयोजित करने पर केवल एक ही क्रम प्राप्त हो तो दिये गए निष्कर्षों में से जो भी निष्कर्ष इन्हें अनुसरण करेंगे वह बिल्कुल ही सत्य माना जाएगा।
- यदि कथनों को संयोेजित करने पर केवल एक ही क्रम प्राप्त होता हो लेकिन दिये गए निष्कर्षों में से कोई भी इसे अनुसरण नहीं करता हो तो ऐसा निष्कर्ष असत्य माना जाएगा।
- यदि कथनों को संयोजित करने पर दो संभावित स्थितियाँ प्राप्त होती हों तो ऐसी स्थिति में:
- यदि दिया गया कोई निष्कर्ष दोनों ही स्थितियों को समान रूप से अनुसरण करता हो तो ऐसा निष्कर्ष निश्चित रूप से सत्य माना जाएगा।
- यदि दिया गया निष्कर्ष केवल एक ही संभावित स्थिति को अनुसरण करता हो, तो ऐसा निष्कर्ष असत्य माना जाएगा।
- यदि दिये गए दोनों ही निष्कर्ष अलग-अगल संभावित स्थितियों को अनुसरण करते हों पर इनमें प्रयुक्त अवयव भिन्न हों तो ऐसा निष्कर्ष निश्चित रूप से असत्य माना जाएगा।
- यदि दिये गए दोनों ही निष्कर्ष अलग-अलग संभावित स्थितियों को अनुसरण करते हों साथ ही इनमें प्रयुक्त अवयव समान हों (जैसे- P > Q @ P = Q) तो ऐसे निष्कर्ष या तो I या II के रूप में सत्य माने जायेंगे।
साधित उदाहरण (Solved Examples)
उदाहरण 1-5: निम्नलिखित प्रश्नों में $, #, @, © और % प्रतीक नीचे बताए गए अर्थों में प्रयोग किए गए हैं:
- ‘P @ Q’ का अर्थ ‘P, Q से छोटा नहीं है’।
- ‘P $ Q’ का अर्थ है ‘P, Q’ से बड़ा नहीं है’।
- ‘P % Q’ का अर्थ है ‘P, Q’ से न तो बड़ा है न बराबर है’।
- ‘P # Q’ का अर्थ है ‘P, Q से न तो छोटा है न बराबर है’।
- ‘P © Q’ का अर्थ है ‘P, Q से न तो छोटा है न बड़ा है’।
अब निम्नलिखित में से प्रत्येक प्रश्न में दिए गए कथन को सत्य मानते हुए पता लगाइए कि दिए गए निष्कर्षों I व II में से कौन-सा/से निश्चित रूप से सत्य है/हैं ?
1. कथनः H @ M, M $ D, D % N
निष्कर्षः
I. N # M
II. N © H
- केवल निष्कर्ष I सत्य है।
- केवल निष्कर्ष II सत्य है।
- या तो निष्कर्ष I या II सत्य है।
- न तो निष्कर्ष I न ही II सत्य है।
- दोनों निष्कर्ष I और II सत्य हैं।
हल (1): 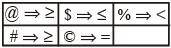
H @ M ⇒ H ≥ M
M $ D ⇒ M ≤ D
D % N ⇒ D < Nअतः, H ≥ M ≤ D < Nनिष्कर्ष I. N # M ⇒ N > M: सत्य
निष्कर्ष II. N © H ⇒ N = H: असत्य
2. कथनः R # T, T @ J, J © B
निष्कर्षः
I. B $ T
II. J % R
- केवल निष्कर्ष I सत्य है।
- केवल निष्कर्ष II सत्य है।
- या तो निष्कर्ष I या II सत्य है।
- न तो निष्कर्ष I न ही II सत्य है।
- दोनों निष्कर्ष I और II सत्य हैं।
हल (5): R # T ⇒ R > T
T @ J ⇒ T ≥ J
J © B ⇒ J = B
अतः R > T > J = B
निष्कर्ष I. B $ T ⇒ B ≤ T: सत्य
निष्कर्ष II. J % R ⇒ J < R: सत्य
3. कथनः M $ K, K # W, R @ W
निष्कर्षः
I. M % W
II. R # K
- केवल निष्कर्ष I सत्य है।
- केवल निष्कर्ष II सत्य है।
- या तो निष्कर्ष I या II सत्य है।
- न तो निष्कर्ष I न ही II सत्य है।
- दोनों निष्कर्ष I और II सत्य हैं।
हल (4): M $ K ⇒ M ≤ K K # W ⇒ K > W
R @ W ⇒ R ≥ W
अतः M ≤ K > W ≤ R
निष्कर्ष I. M % W ⇒ M < W: असत्य निष्कर्ष II. R # K ⇒ R > K: असत्य
4. कथनः Z © T, T % D, D # K
निष्कर्षः
I. K % Z
II. D # K
- केवल निष्कर्ष I सत्य है।
- केवल निष्कर्ष II सत्य है।
- या तो निष्कर्ष I या II सत्य है।
- न तो निष्कर्ष I न ही II सत्य है।
- दोनों निष्कर्ष I और II सत्य हैं।
हल (2): Z © T ⇒ Z = T
T % D ⇒ T < D, D # K ⇒ D > K
अत: = T < D > K
निष्कर्ष I. K % Z ⇒ K < Z : असत्य निष्कर्ष II. D # Z ⇒ D > Z : सत्य
5. कथनः A % F, F © R, R $ B
निष्कर्षः
I. A % B
II. B @ F
- केवल निष्कर्ष I सत्य है।
- केवल निष्कर्ष II सत्य है।
- या तो निष्कर्ष I या II सत्य है।
- न तो निष्कर्ष I न ही II सत्य है।
- दोनों निष्कर्ष I और II सत्य हैं।
हल (5): A % F ⇒ A < FF © R ⇒ F = RR $ B ⇒ R ≤ Bअतः, A < F = R ≤ Bनिष्कर्ष I. A % B ⇒ A < B: सत्य निष्कर्ष I.B @ F ⇒ B ≥ F: सत्य
निर्देश (6-10): निम्नलिखित प्रश्नों में प्रतीक @, ©, %, $ और * को निम्नानुसार अर्थों में प्रयुक्त किया गया है:
- ‘P © Q’ का अर्थ है ‘P, Q से बड़ा नहीं है।’
- ‘P & Q’ का अर्थ है ‘P, Q से छोटा नहीं है।’
- ‘P % Q’ का अर्थ है ‘P न तो Q से बड़ा और न ही समान है।’
- ‘P $ Q’ का अर्थ है ‘P न तो Q से छोटा और न ही समान है।’
- ‘P @ Q’ का अर्थ है ‘P न तो Q से बड़ा और न ही छोटा है।’
निम्नलिखित प्रत्येक प्रश्न में दिए गए कथनों को सत्य मानते हुए, पता लगाइए कि उनके नीचे दिए गए तीन निष्कर्ष I, II और III में से कौन-सा/कौन-से निश्चित रूप से सत्य है/हैं?
6. कथन: J $ D, D © K, K % R
निष्कर्ष:
I. R $ J
II. R $ D
III. K $ J
- कोई कथन नहीं है
- केवल I सत्य है
- केवल II सत्य है
- केवल III सत्य है
- केवल II और III सत्य हैं
हल (3): J > D, D ≤ K, K < R सभी को मिलाने पर J > D ≤ K < R या R > D
अतः केवल II सत्य है।
7. कथन: M & K, K @ R, R % N
निष्कर्षः
I. R % M
II. R @ M
III. N $ K
- केवल I सत्य है
- केवल II सत्य है
- केवल III सत्य है
- केवल या तो I या II सत्य है
- केवल या तो I या II और III सत्य है
हल (5): M ≥ K, K = R, R < Nसभी को मिलाने परM ≥ K = R < N या R ≤ M और N > K
अतः या तो I या II और III सत्य है।
8. कथन: B % H, H $ J, J & M
निष्कर्ष:
I. B % J
II. M % B
III. H $ M
- कोई सत्य नहीं है
- केवल I सत्य है
- केवल II सत्य है
- केवल III सत्य है
- केवल II और III सत्य हैं
हल (4): B < H, H > J, J ≥ M
सभी को मिलाने पर
B < H > J ≥ M
या H > M
अतः केवल III सत्य है।
9. कथन: Z © K, K % E, E @ R
निष्कर्ष:
I. R $ K
II. Z % E
III. R $ Z
- केवल I सत्य है
- केवल I और II सत्य हैं
- केवल I और III सत्य हैं
- केवल II और III सत्य हैं
- I, II और III सभी सत्य हैं
हल (5): Z ≤ K, K < E, E = Rसभी को मिलाने परZ ≤ K < E = R या R > K, Z < E और R > Z
अतः सभी सत्य हैं।
10. कथन: W @ M, M © R, R $ F
निष्कर्ष:
I. F % M
II. R & W
III. W % F
- कोई सत्य नहीं है
- केवल I सत्य है
- केवल II सत्य है
- केवल III सत्य है
- केवल I और II सत्य हैं
हल (3): W = M, M ≤ R, R > F
सभी को मिलाने पर
W = M ≤ R > F या R ≥ W
अतः केवल II सत्य है।