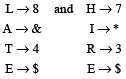काल परीक्षा (Clock And Calendar Test) शार्ट ट्रिक और उदहारण
काल परीक्षण में आपसे कैलेण्डर, घड़ी और समय संबंधी प्रश्न पूछे जाते हैं। इसके लिए आपको कैलेण्डर, घड़ी और समय का ज्ञान पूर्णतः होना चाहिए। कुछ आवश्यक जानकारियाँ निम्नलिखित हैं:
- सप्ताह में सात दिन होते हैं – रविवार, सोमवार, मंगलवार, बुधवार, बृहस्पतिवार, शुक्रवार तथा शनिवार।
- एक वर्ष में बारह महीने होते हैं – जनवरी (31 दिन), फरवरी (28 या 29 दिन), मार्च (31 दिन), अप्रैल (30 दिन), मई (31 दिन), जून (30 दिन), जुलाई (31 दिन), अगस्त (31 दिन), सितम्बर (30 दिन), अक्टूबर (31 दिन), नवम्बर (30 दिन), दिसम्बर (31 दिन)।
- यदि कोई वर्ष 4 से पूर्णतः विभाजित हो जाता है, तो वह वर्ष ‘लीप वर्ष’ कहलाता है।
- साधारणतः फरवरी 28 दिन का होता है, परन्तु लीप वर्ष में फरवरी 29 दिन का होता है।
- एक वर्ष में 52 सप्ताह तथा एक दिन होते हैं तथा लीप वर्ष में 52 सप्ताह तथा दो दिन होते हैं।
- दिनों की संख्या को सात से भाग देने पर जो शेष बचता है, उसे विषम दिन कहते हैं।
- एक दिन या वार की पुनरावृत्ति प्रत्येक 7, 14, 21, 28, … 364 दिनों के बाद होती है।
- घड़ी की सूइयाँ जब अपने वृत्ताकार मार्ग पर एक पूर्ण चक्कर लगाती है, तब उन्हें 360° घूमना पड़ता है।
- एक मिनट की दूरी 6° के बराबर होता है।
- जब मिनट की सूई एक मिनट की दूरी तय करती है, तो घण्टे की सूई 1/2° के बराबर आगे बढ़ जाती है।
- एक घण्टा में 60 मिनट तथा 1 मिनट में 60 सेकण्ड होते हैं।
- प्रत्येक एक घण्टे में मिनट की सूई घण्टे की सूई से 55 मिनट दूरी आगे बढ़ जाती है।
- प्रत्येक घण्टे में दोनों सूइयाँ एक ही दिशा में एक बार मिलती हैं, लेकिन 12 घण्टें में 11 बार तथा 24 घण्टे में 22 बार मिलती हैं।
- प्रत्येक घण्टे में दोनों सूइयाँ केवल एक बार विपरीत दिशा में होती हैं, लेकिन 12 घण्टे में 11 बार तथा 24 घण्टे में 22 विपरीत होती हैं।
- प्रत्येक घण्टे में दोनों सूइयाँ दो बार समकोण बनाती हैं, लेकिन 12 घण्टे में 24 बार परस्पर समकोण बनाती हैं।
- प्रत्येक घण्टे में दोनों सूइयाँ दो बार समकोण बनाती हैं तथा इस दशा में दोनों सूइयों के बीच की दूरी 15 मिनट के बराबर होती है।
पूछे जाने वाले प्रश्नों पर एक दृष्टि
उदाहरण 1. यदि किसी महीने की तीसरी तारीख को मंगलवार है, तो उसी महीने की 27 तारीख से चार दिन पहले कौन-सा दिन होगा?
- मंगलवार
- सोमवार
- बुधवार
- रविवार
हल (2): 27 – 3 = 24
विषम दिनों की कुल संख्या = 3
मंगलवार + 3 ⇒ शुक्रवार – 4 ⇒ सोमवार
उदाहरण 2. प्रकाश को याद है कि उसके पिताजी का जन्मदिन 13 और 16 अप्रैल के बीच किसी दिन है, जबकि उसकी बहन को याद है कि उसके पिताजी का जन्म-दिन 14 अप्रैल के बाद लेकिन 17 अप्रैल के पहले किसी दिन है। बताएँ कि इनके पिताजी का जन्म दिन किस दिन को है?
- 14 अप्रैल
- 15 या 16 अप्रैल
- 14 या 15 अप्रैल
- 15 अप्रैल
हल (4):
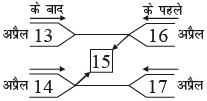
अतः, अभीष्ट तिथि ⇒ 15 अप्रैल।
चूँकि दोनों कथनानुसार 13 और 14 के बाद एवं 16 तथा 17 के पहले वो तिथि है। अर्थात् 13, 14, 16 एवं 17 ये तिथियाँ अमान्य हो जाएँगी। इसलिए अब हम देखेंगे कि 14 एवं 16 के बीच कौन सी तिथि है। हम जानते हैं कि 14 एवं 16 के बीच में केवल 15 एक तिथि है तथा दोनों कथनों में भी केवल 15 ही एक ऐसी तिथि है जो कि उभयनिष्ठ है।
सूक्ष्म विधि
अभीष्ट तिथि = दोनों तिथियों में, ‘के बाद’ में प्रयुक्त तिथियों में से बड़ी तिथि + 1
= 14 + 1 ⇒ 15 या
अभीष्ट तिथि = दोनों तिथियों में, ‘के पहले’ प्रयुक्त तिथियों में से छोटी तिथि – 1
= 16 – 1 ⇒ 15
अतः प्रकाश के पिताजी का जन्म-दिन 15 अप्रैल को है।
उदाहरण 3. प्रशिक्षक महोदय 8:35 बजे खेल के मैदान में पहुँचे। राजेश 45 मिनट देर से पहुँचा और इस प्रकार वह प्रशिक्षण के समय से 15 मिनट देर था। बताएँ कि प्रशिक्षक महोदय निर्धारित समय से कितने मिनट पहले पहुँचे थे?
- 15 मिनट
- 30 मिनट
- 45 मिनट
- 25 मिनट
हल (2): प्रशिक्षक महोदय के पहुँचने का समय → 8:35
राकेश 45 मिनट देर से पहुँचा → +45 मिनट
∴ राकेश के पहुँचने का समय = 9:20
राकेश प्रशिक्षण के निर्धारित समय से देर → -15 मिनट
∴ प्रशिक्षण का निर्धारित समय = 9:05
चूँकि प्रशिक्षण का निर्धारण समय 9:05 है, और प्रशिक्षक महोदय 8:35 में ही पहुँच गये थे।
अतः वे प्रशिक्षण के निर्धारित समय से (9:05 – 8:35 ⇒ 30) 30 मिनट पहले पहुँचे थे।
चूँकि प्रशिक्षक महोदय 8:35 बजे पहुँचे हैं और राकेश उनसे 45 मिनट देर से पहुँचा यानी राकेश (8:35 + 45 = 9:20) 9:20 बजे पहुँचा फिर भी वह प्रशिक्षण के निर्धारित समय से 15 मिनट विलम्ब था, यानी प्रशिक्षण का निर्धारित समय (9:20 – 15 = 9:05 =) 9:05 बजे है। चूँकि प्रशिक्षक महोदय के पहुँचने का समय 8:35 बजे है। अतः प्रशिक्षक महोदय निर्धारित समय (9:05 – 8:35 = 30) से 30 मिनट पहले पहुँचे थे।
सूक्ष्म विधि
8:35 + 30 – 8:35 ⇒ 30 मिनट या
45 – 15 ⇒ 30 मिनट
साधित उदाहरण (Solved Examples)
1. इस वर्ष बालू का जन्मदिन 27 जनवरी अर्थात् बुधवार को पड़ता है। बालू को याद है कि मोहन का जन्मदिन उसके जन्मदिन के बाद ठीक पांचवे शुक्रवार को पड़ता है। मोहन बालू से कितना छोटा है?
- आंकडे अधूरे हैं
- 30 दिन
- 31 दिन
- 29 दिन
हल (2): बुधवार के दो दिन बाद पहला शुक्रवार होगा। दिनों की कुल संख्या
= 2 + (7 × 4) = 30 दिन
2. शैलेश ने सोमवार को फिल्म देखी। नितिन ने विकास से दो दिन पहले किंतु शैलेश से तीन दिन बाद फिल्म देखी। विकास ने किस दिन फिल्म देखी?
- सोमवार
- शनिवार
- मंगलवार
- रविवार
हल (2): नितिन ने सोमवार + 3 = बृहस्पतिवार को फिल्म देखी।
विकास ने बृहस्पतिवार + 2 = शनिवार को फिल्म देखी।

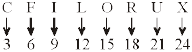

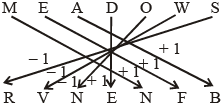
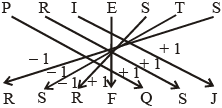


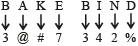



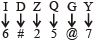
 शर्त (iii) लागू होती है।
शर्त (iii) लागू होती है। शर्त (iii) लागू होती है।
शर्त (iii) लागू होती है। शर्त (ii) लागू होती है।
शर्त (ii) लागू होती है। शर्त (i) लागू होती है।
शर्त (i) लागू होती है।