Measurement of Length

Measurement of Length

You are already familiar with some direct methods for the measurement of length. For example, a metre scale is used for lengths from 10–3 m to 102 m. A vernier callipers is used for lengths to an accuracy of 10–4 m. A screw gauge and a spherometer can be used to measure lengths as less as to 10–5 m. To measure lengths beyond these ranges, we make use of some special indirect methods.

 Measurement of Large Distances

Large distances such as the distance of a planet or a star from the earth cannot be measured directly with a metre scale. An important method in such cases is the parallax method.

When you hold a pencil in front of you against some specific point on the background (a wall) and look at the pencil first through your left eye A (closing the right eye) and then look at the pencil through your right eye B (closing the left eye), you would notice that the position of the pencil seems to change with respect to the point on the wall. This is called parallax. The distance between the two points of observation is called the basis. In this example, the basis is the distance between the eyes. 

To measure the distance D of a far away planet S by the parallax method, we observe it from two different positions (observatories) A and B on the Earth, separated by distance AB = b at the same time as shown in Fig. 2.2. We measure the angle between the two directions along which the planet is viewed at these two points. The ∠ASB in Fig. 2.2 represented by symbol θ is called the parallax angle or parallactic angle.

As the planet is very far away,

b/D <<1

and therefore, 

D = b/θ

is very small. Then we approximately take AB as an arc of length b of a circle with centre at S and the distance D as the radius AS = BS so that AB = b = D θ  where θ  is in radians.

(2.1)

Having determined D, we can employ a similar method to determine the size or angular diameter of the planet. If d is the diameter of the planet and α  the angular size of the planet (the angle subtended by d at the earth), we have 

α = d/D (2.2)

Fig. 2.2  Parallax method.

The angle α  can be measured from the same location on the earth. It is the angle between the two directions when two diametrically opposite points of the planet are viewed through the telescope. Since D is known, the diameter d of the planet can be determined using Eq. (2.2).

Estimation of Very Small Distances: Size of a Molecule

To measure a very small size, like that of a molecule (10–8 m to 10–10 m), we have to adopt special methods. We cannot use a screw gauge or similar instruments. Even a microscope has certain limitations. An optical microscope uses visible light to ‘look’ at the system under investigation. As light has wave like features, the resolution to which an optical microscope can be used is the wavelength of light (A detailed explanation can be found in the Class XII Physics textbook). For visible light the range of wavelengths is from about 4000 Å to 7000 Å 

(1 angstrom = 1 Å = 10-10 m). Hence an optical microscope cannot resolve particles with sizes smaller than this. Instead of visible light, we can use an electron beam. Electron beams can be focussed by properly designed electric and magnetic fields. The resolution of such an electron microscope is limited finally by the fact that electrons can also behave as waves . The wavelength of an electron can be as small as a fraction of an angstrom. Such electron microscopes with a resolution of 0.6 Å have been built. They can almost resolve atoms and molecules in a material. In recent times, tunnelling microscopy has been developed in which again the limit of resolution is better than an angstrom. It is possible to estimate the sizes of molecules. 

A simple method for estimating the molecular size of oleic acid is given below. Oleic acid is a soapy liquid with large molecular size of the order of 10–9 m.

The idea is to first form mono-molecular layer of oleic acid on water surface. 

We dissolve 1 cm3 of oleic acid in alcohol to make a solution of 20 cm3. Then we take 1 cm3 of this solution and dilute it to 20 cm3, using alcohol. So, the concentration of the solution is equal to  

(1/20×20) cm³

  of oleic acid/cm3 of solution. Next we lightly sprinkle some lycopodium powder on the surface of water in a large trough and we put one drop of this solution in the water. The oleic acid drop spreads into a thin, large and roughly circular film of molecular thickness on water surface. Then, we quickly measure the diameter of the thin film to get its area A. Suppose we have dropped n drops in the water. Initially, we determine the approximate volume of each drop (V cm3).

Volume of n drops of solution 

= nV cm3 

Amount of oleic acid in this solution

= 

nV(1/20×20) cm³

This solution of oleic acid spreads very fast on the surface of water and forms a very thin layer of thickness t. If this spreads to form a film of area A cm2, then the thickness of the film

t = Volume of the film /Area of the film

or, 

t = nV(1/20×20A) cm

(2.3)

If we assume that the film has mono-molecular thickness, then this becomes the size or diameter of a molecule of oleic acid. The value of this thickness comes out to be of the order of 10–9 m.

The International System of Units

The International System of Units

In earlier time scientists of different countries were using different systems of units for measurement. Three such systems, the CGS, the FPS (or British) system and the MKS system were in use extensively till recently.

The base units for length, mass and time in these systems were as follows :

• In CGS system they were centimetre, gram and second respectively.

• In FPS system they were foot, pound and second respectively.

• In MKS system they were metre, kilogram and second respectively. 

The system of units which is at present internationally accepted for measurement is the Système Internationale 

d’ Unites (French for International System of Units), abbreviated as SI. The SI, with standard scheme of symbols, units and abbreviations, developed by the Bureau International des Poids et measures (The International Bureau of weights and measures, BIPM) in 1971 were recently revised by the General Conference on weights and measures in November 2018. The scheme is now for international usage in scientific, technical, industrial and commercial work. Because SI units used decimal system, conversions within the system are quite simple and convenient. We shall follow the SI units in this book.

In SI, there are seven base units as given in  Table 2.1. Besides the seven base units, there are two more units that are defined for (a) plane angle dθ as the ratio of length of arc ds to the radius r and (b) solid angle dΩ as the ratio of the intercepted area dA of the spherical surface, described about the apex O as the centre, to the square of its radius r, as shown in Fig. 2.1(a) and (b) respectively. The unit for plane angle is radian with the symbol rad and the unit for the solid angle is steradian with the symbol sr. Both these are dimensionless quantities.

Fig.  2.1 Description  of  (a)  plane  angle  dθ  and  (b)  solid  angle

Table 2.1  SI Base Quantities and Units*

* The values mentioned here need not be remembered or asked in a test. They are given here only to indicate the extent of accuracy to which they are measured. With progress in technology, the measuring techniques get improved leading to measurements with greater precision. The definitions of base units are revised to keep up with this progress.

  

Table 2.2 Some units retained for general use (Though outside SI)

Note that when mole is used, the elementary entities must be specified. These entities may be atoms, molecules, ions, electrons, other particles or specified groups of such particles. 

We employ units for some physical quantities that can be derived from the seven base units (Appendix A 6). Some derived units in terms of the SI base units are given in (Appendix A 6.1). Some SI derived units are given special names (Appendix A 6.2 ) and some derived SI units make use of these units with special names and the seven base units (Appendix A 6.3). These are given in Appendix A 6.2 and A 6.3 for your ready reference. Other units retained for general use are given in Table 2.2.

Common SI prefixes and symbols for multiples and sub-multiples are given in Appendix A2. General guidelines for using symbols for physical quantities, chemical elements and nuclides are given in Appendix A7 and those for SI units and some other units are given in Appendix A8 for your guidance and ready reference.

Coulomb’s Law

Coulomb’s Law

Coulomb’s law is a quantitative statement about the force between two point charges. When the linear size of charged bodies are much smaller than the distance separating them, the size may be ignored and the charged bodies are treated as point charges. Coulomb measured the force between two point charges and found that it varied inversely as the square of the distance between the charges and was directly proportional to the product of the magnitude of the two charges and acted along the line joining the two charges. Thus, if two point charges q1, q2 are separated by a distance r in vacuum, the magnitude of the force (F) between them is given by 

F =|q1×q2|/r²

How did Coulomb arrive at this law from his experiments? Coulomb used a torsion balance* for measuring the force between two charged metallic spheres. When the separation between two spheres is much larger than the radius of each sphere, the charged spheres may be regarded as point charges.

Basic Properties of Electric Charge

1.5 Basic Properties of Electric Charge

We have seen that there are two types of charges, namely positive and negative and their effects tend to cancel each other. Here, we shall now describe some other properties of the electric charge. 

If the sizes of charged bodies are very small as compared to the distances between them, we treat them as point charges. All the  charge content of the body is assumed to be concentrated at one point  in space.

1.5.1 Additivity of charges

We have not as yet given a quantitative definition of a charge; we shall follow it up in the next section. We shall tentatively assume that this can be done and proceed. If a system contains two point charges q1 and q2, the total charge of the system is obtained simply by adding algebraically q1 and q2 , i.e., charges add up like real numbers or they are scalars like the mass of a body. If a system contains n charges q1, q2, q3, …, qn, then the total charge of the system is q1 + q2 + q3 + … + qn . Charge has magnitude but no direction, similar to mass. However, there is one difference between mass and charge. Mass of a body is always positive whereas a charge can be either positive or negative. Proper signs have to be used while adding the charges in a system. For example, the  total charge of a system containing five charges +1, +2, –3, +4 and –5,  in some arbitrary unit, is (+1) + (+2) + (–3) + (+4) + (–5) = –1 in the  same unit.

1.5.2 Charge is conserved

We have already hinted to the fact that when bodies are charged by rubbing, there is transfer of electrons from one body to the other; no new charges are either created or destroyed. A picture of particles of electric charge enables us to understand the idea of conservation of charge. When we rub two bodies, what one body gains in charge the other body loses. Within an isolated system consisting of many charged bodies, due to interactions among the bodies, charges may get redistributed but it is found that the total charge of the isolated system is always conserved. Conservation of charge has been established experimentally.

It is not possible to create or destroy net charge carried by any isolated system although the charge carrying particles may be created or destroyed in a process. Sometimes nature creates charged particles: a neutron turns into a proton and an electron. The proton and electron thus created have equal and opposite charges and the total charge is zero before and after the creation. 

1.5.3 Quantisation of charge

Experimentally it is established that all free charges are integral multiples of a basic unit of charge denoted by e. Thus charge q on a body is always given by

q = ne

where n is any integer, positive or negative. This basic unit of charge is the charge that an electron or proton carries. By convention, the charge on an electron is taken to be negative; therefore charge on an electron is written as –e and that on a proton as +e. 

The fact that electric charge is always an integral multiple of e is termed as quantisation of charge. There are a large number of situations in physics where certain physical quantities are quantised. The quantisation of charge was first suggested by the experimental laws of electrolysis discovered by English experimentalist Faraday. It was experimentally demonstrated by Millikan in 1912. 

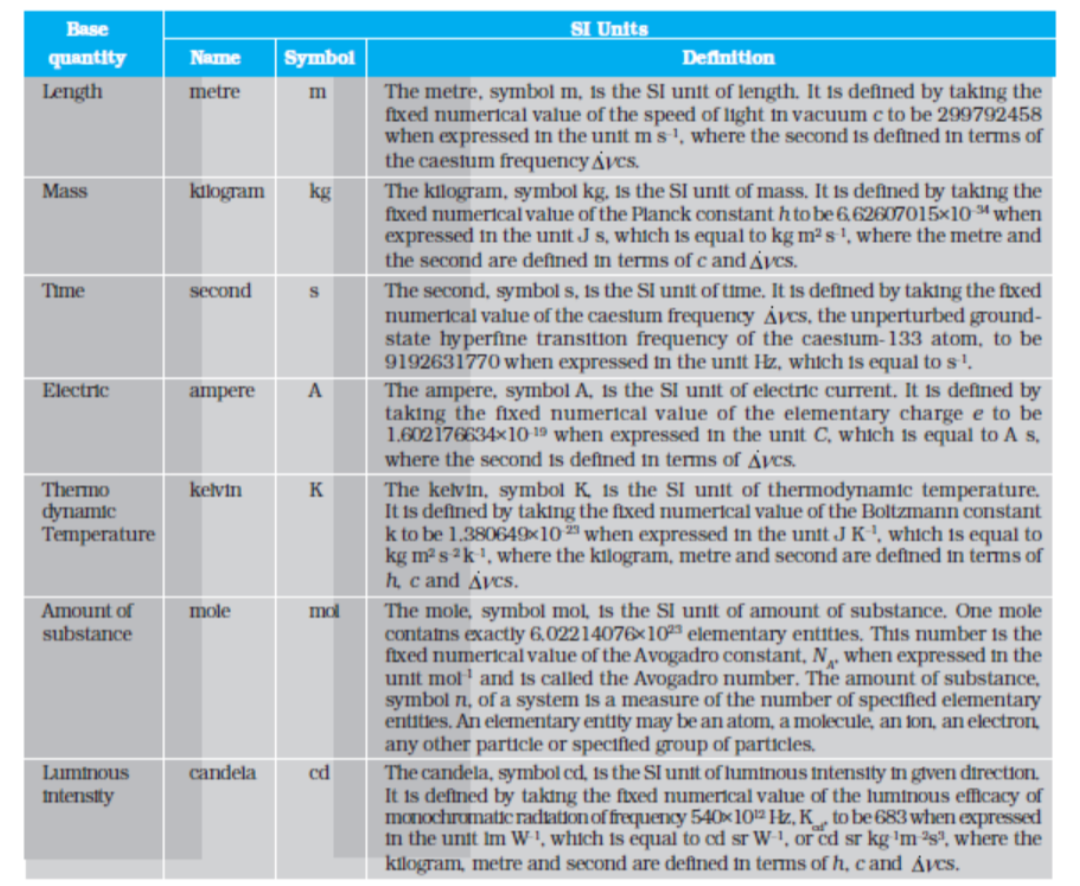
In the International System (SI) of Units, a unit of charge is called a coulomb and is denoted by the symbol C. A coulomb is defined in terms the unit of the electric current which you are going to learn in a subsequent chapter. In terms of this definition, one coulomb is the charge flowing through a wire in 1 s if the current is 1 A (ampere), (see Chapter 2 of Class XI, Physics Textbook , Part I). In this system, the value of the basic unit of charge is 

e = 1.602192 × 10–19 C

Thus, there are about 6 × 1018 electrons in a charge of –1C. In electrostatics, charges of this large magnitude are seldom encountered and hence we use smaller units 1 µC (micro coulomb) = 10–6 C or 1 mC (milli coulomb) = 10–3 C. 

If the protons and electrons are the only basic charges in the universe, all the observable charges have to be integral multiples of e. Thus, if a body contains n1 electrons and n2 protons, the total amount of charge on the body is n2 × e + n1 × (–e) = (n2 – n1) e. Since n1 and n2 are integers, their difference is also an integer. Thus the charge on any body is always an integral multiple of e and can be increased or decreased also in steps of e. 

The step size e is, however, very small because at the macroscopic level, we deal with charges of a few µC. At this scale the fact that charge of a body can increase or decrease in units of e is not visible. In this respect, the grainy nature of the charge is lost and it appears to be continuous.

This situation can be compared with the geometrical concepts of points and lines. A dotted line viewed from a distance appears continuous to us but is not continuous in reality. As many points very close to each other normally give an impression of a continuous line, many  small charges taken together appear as a continuous charge  distribution.

At the macroscopic level, one deals with charges that are enormous compared to the magnitude of charge e. Since e = 1.6 × 10–19 C, a charge of magnitude, say 1 µC, contains something like 1013 times the electronic charge. At this scale, the fact that charge can increase or decrease only in units of e is not very different from saying that charge can take continuous values. Thus, at the macroscopic level, the quantisation of charge has no practical consequence and can be ignored. However, at the microscopic level, where the charges involved are of the order of a few tens or hundreds of e, i.e., they can be counted, they appear in discrete lumps and quantisation of charge cannot be ignored. It is the magnitude of scale involved that is very important.

Mathematics MCQ Class 12

CBSE Class 12 2023 : Maths Important MCQs for CBSE Board Exam 2023

In this post, CBSE Board 12th Maths Exam 2023 Important MCQs Question Answers have been given.

The purpose of these practice questions and answers is to help the students prepare for their exams and perform well in them.

It is advised to read this resource before the actual paper as it can give students an idea about the type of questions they can expect in the exam.

1 The number of equivalence relations that can be defined in the set A= {1,2,3} which containing the elements (1,2) is

(a) 0

(b) 1

(c) 2

(d) 3

2 The number of one-to-one functions that can be defined from the set {1,2,3,4,5} to {a, b}

a) 5

b) 0

c) 2

d) 3

3 What is the simplified form of cos-1(4x3 − 3x)

(a) 3sin−1 x

(b) 3cos−1 x

(c) π − 3 sin−1 x

(d) π − 3 cos−1 x

4 The number of all possible matrices of order2x3 with entry 1 or 2

1)16

2) 64

3) 6

4) 24

5 If the order of matrix P is 2x3 and the order of matrix Q is 3x4 , find the order of PQ.

1) 2x4

2) 2x2

3) 4x2

4) 3x3

6 Let A is a non – singular matrix of order 3 x 3 then | A ( adj A )| is equal to

a)| A |

b)| A |2

c)| A |3

d)3| A |

7 The function f(x) =[x] is continuous at

a)4

b)-2

c)1

d)1.5

8 The bottom of a rectangular swimming tank is 25 m by 40 m water is pumped into the tank at the rate of 500 cubic meters per minute. Find the rate at which the level of water in the tank is rising?

A) 1⁄4 m/min

B) 2/3 m/min

C) 1/3 m/min

D) 1⁄2 m/min

9 Area of region bound by circle x2+y2=1

a)2 sq units

b) sq units

c)3 sq units

d)4 sq units

10 Integrating factor of the differential equation dy/dx + y tan x – sec x = 0 is:

(A) cosx 

(B) secx 

(C) ecosx

(D) esecx

11 If points A (60 î+ 3 ĵ), (40 î– 8 ĵ) and C ( aî- 52ĵ) are collinear, then ‘a’ is equal to

a) 40

b) -40

c) 20

d) -20

12 Write direction cosines of a line parallel to z-axis.

(a) 1,0,0

(b) 0,0,1

(c) 1,1,0

(d) -1,-1,-1

13 Find the foot of the perpendicular drawn from the point (2,-3,4) on the y-axis.

(a) (2,0,4)

(b) (0.3.0)

(c) (0,-3,0)

(d) (-2,0,-4)

14 If α,β, Υ are the angles that a line makes with the positive direction of x,y,z axis respectively then the direction cosines of the line are

(a) cosα,sinβ, cosΥ

(b) cosα,cosβ, cosΥ

(c) sinα,sinβ, sinΥ

(d) 1, 1, 1

15 The feasible region of the inequality x+y≤1 and x–y≤1 lies in......... quadrants.

(a)Only I and II 

(b)Only I and III

(c)Only II and III

(d)All four

16 Two dice are thrown. If it is known that the sum of numbers on the dice was less than 6, the probability of getting a sum 3 is

a)1/18

b)5/18

c)1/5

d)2

17 The solution set of the inequality 3x + 5y < 4 is

a)an open half-plane not containing the origin.

b)an open half-plane containing the origin.

c)the whole XY-plane not containing the line 3x + 5y = 4.

d)a closed half plane containing the origin.

18 If A is a square matrix of order 3 and |A| = 5, then |adjA| =

(a) 5

(b) 25

(c) 125

(d) ⅕

19 The area of a triangle with vertices (2, −6), (5,4) and (k, 4) is 35 square units then , k is

A.12

B. −2

C. −12, −2

D. 12, −2

20 The vector having initial and terminal points as (2,5,0) and (-3,7,4) respectively is

A. 5î+ 2ĵ− 4k̂

B. −î+ 12ĵ+ 4k̂

C. −5î+ 2ĵ+ 4k̂

D.−5î+ 12ĵ+ 4k̂

21. Let A = { 1 , 2, 3 } and consider the relation R = {(1 , 1), (2 , 2), ( 3 , 3), (1 , 2), (2 , 3), (1,3)} Then , R is

(a) Reflexive but not symmetric

(b) Reflexive but not transitive

(c) Symmetric and transitive

(d)Neither symmetric nor transitive

22. If A is a skew – symmetric matrix , then A² is

(a) Symmetric

(b) Skew – symmetric

(c) A² = A

(d) A² ≠ A

23. The number of arbitrary constants in the general solution of a differential equation of fourth order are :

(a) 0

(b) 2

(c) 3

(d) 4

24. If y = log x/ (1+x) , then dy/ dx is equal to

(a) x/ (1+x)²

(b) 1/ (1+x) ²

(c) 2x/ (1+x)²

(d) 1/ x(1+x)

25. Corner points of the region for an LPP are (0, 2), (3, 0), (6, 0),(6, 8), and (0, 5) . Let F = 4x + 6y be the objective function. The minimum value of F occurs at

(a) (0,2) only

(b)(3,0) only

(c) The midpoint of the line segment joining the points (0,2) and ( 3, 0) only

(d) Any point on the line segment joining the points (0,2) and (3, 0) only.

26. f(x) = xˣ has a stationary point at

(a) x = e

(b) x = 1/ e

(c) x = 1

(d) x = √e

27. If A and B are events such that P ( A/ B) = P (B/ A) , then ………

(a) P(A) = P(B)

(b) P(A) ≠ P(B)

(c) P(A) + P(B) = 1

(d) None of these

28. If R = {(x , y ): x + 2y = 8 } is a relation N , then the range of R is :

(a){3, 2 , 1}

(b) { 3 , 2}

(c) {2 , 8 , 1}

(d) {3}

29. Let f ∶ R → R be defined as f(x) = 3x. Choose the correct answer.

(a) f is one – one onto

(b) f is many-one onto

(c) f is one – one but not onto

(d) f is neither one-one nor onto

30. The principal value of [tan-1 √3 − cot-1, (−√3)] is :

(a)π

(b) − π/2

(c) 0

(d) 2√3

31. If cos (sin-1 2/ 5 + cos-1 x) = 0 , then x is equal to

(a) 1/ 5

(b)2/ 5

(c) 0

(d) 1

32. The value of ∫ (cos 2x)/ (sinx +cosx)² dx is

(a) log | cos x + sin x | + C

(b) log | cos x − sin x | + C

(c) log | cos x + sin x |² + C

(d) log | cos x + sin x |-2 + C

33. The derivative of 3ˣ  w.r.t x is :

(a) log 3

(b) x. 3ˣ-1

(c) 0

(d) 3ˣ log 3

34. A is a square matrix of order 2, then adj(adj A) is :

(a) O

(b) I

(c) A-1

(d) A

35. The number of arbitrary constants in the general solution of a differential equation of fourth order is :

(a) 1

(b) 2

(c) 3

(d) 4

 

📖🖋️

1. Chemical Reactions and Equations

Chemical Equations 

When a magnesium ribbon is burnt in oxygen, it gets converted to magnesium oxide. This description of a chemical reaction in a sentence form is quite long. It can be written in a shorter form. The simplest way to do this is to write it in the form of a word-equation.

The word-equation for the above reaction would be –

Magnesium + Oxygen → 

(reactants)

Magnesium Oxide 

(product)

The substances that undergo chemical change in the reaction, magnesium and oxygen, are the reactants. The new substance is magnesium oxide, formed during the reaction, as a product.

A word-equation shows change of reactants to products through an arrow placed between them. The reactants are written on the left-hand side (LHS) with a plus sign (+) between them. Similarly, products are written on the right-hand side (RHS) with a plus sign (+) between them. The arrowhead points towards the products, and shows the direction of the reaction.

Writing a Chemical Equation

Chemical equations can be made more concise and useful if we use chemical formulae instead of words. A chemical equation represents a chemical reaction. If you recall formulae of magnesium, oxygen and magnesium oxide, the above word-equation can be written as –

Mg + O2 → MgO

Count and compare the number of atoms of each element on the LHS and RHS of the arrow. Is the number of atoms of each element the same on both the sides? If yes, then the equation is balanced. If not, then the equation is unbalanced because the mass is not the same on both sides of the equation. Such a chemical equation is a skeletal chemical equation for a reaction. Equation is a skeletal chemical equation for the burning of magnesium in air.

Balanced Chemical Equations

Recall the law of conservation of mass that you studied in Class IX; mass can neither be created nor destroyed in a chemical reaction. That is, the total mass of the elements present in the products of a chemical reaction has to be equal to the total mass of the elements present in the reactants.

In other words, the number of atoms of each element remains the same, before and after a chemical reaction. Hence, we need to balance a skeletal chemical equation. Is the chemical Eq balanced? Let us learn about balancing a chemical equation step by step.

The word-equation for Activity may be represented as –

Zinc + Sulphuric acid → Zinc sulphate + Hydrogen

The above word-equation may be represented by the following chemical equation –

Zn + H2SO4 → ZnSO4 + H2 

Let us examine the number of atoms of different elements on both sides of the arrow.

As the number of atoms of each element is the same on both sides of the arrow, Eq.is a balanced chemical equation.

Let us try to balance the following chemical equation –

Fe + H2O → Fe3O4 + H2 

Step I: To balance a chemical equation, first draw boxes around each formula. Do not change anything inside the boxes while balancing the equation.

Step II: List the number of atoms of different elements present in the unbalanced equation.

Step III: It is often convenient to start balancing with the compound that contains the maximum number of atoms. It may be a reactant or a product. In that compound, select the element which has the maximum number of atoms. Using these criteria, we select Fe3O4 and the element oxygen in it. There are four oxygen atoms on the RHS and only one on the LHS.

To balance the oxygen atoms –

To equalise the number of atoms, it must be remembered that we cannot alter the formulae of the compounds or elements involved in the reactions. For example, to balance oxygen atoms we can put coefficient ‘4’ as 4 H2O and not H2O4 or (H2O)4. Now the partly balanced equation becomes–

Step IV: Fe and H atoms are still not balanced. Pick any of these elements to proceed further. Let us balance hydrogen atoms in the partly balanced equation.

To equalise the number of H atoms, make the number of molecules of hydrogen as four on the RHS.

The equation would be –

Step V: Examine the above equation and pick up the third element which is not balanced. You find that only one element is left to be balanced, that is, iron.

To equalise Fe, we take three atoms of Fe on the LHS.

Step VI: Finally, to check the correctness of the balanced equation, we count atoms of each element on both sides of the equation.

The numbers of atoms of elements on both sides of Eq. (1.9) are equal. This equation is now balanced. This method of balancing chemical equations is called hit-and-trial method as we make trials to balance the equation by using the smallest whole number coefficient.

Step VII: Writing Symbols of Physical States Carefully examine the above balanced Eq. (1.9). Does this equation tell us anything about the physical state of each reactant and product? No information has been given in this equation about their physical states.

To make a chemical equation more informative, the physical states of the reactants and products are mentioned along with their chemical formulae. The gaseous, liquid, aqueous and solid states of reactants and products are represented by the notations (g), (l), (aq) and (s), respectively. The word aqueous (aq) is written if the reactant or product is present as a solution in water.

The balanced Eq. (1.9) becomes

3Fe(s) + 4H2O(g) → Fe3O4(s) + 4H2(g) (1.10)

Note that the symbol (g) is used with H2O to indicate that in this reaction water is used in the form of steam.

Usually physical states are not included in a chemical equation unless it is necessary to specify them.

Sometimes the reaction conditions, such as temperature, pressure, catalyst, etc., for the reaction are indicated above and/or below the arrow in the equation. For example 

Using these steps, can you balance Eq. (1.2) given in the text earlier?

Circles

In this chapter, you will be studied the following points:

1. A circle is the collection of all points in a plane, which are equidistant from a fixed point in the plane.

2. Equal chords of a circle (or of congruent circles) subtend equal angles at the centre.

3. If the angles subtended by two chords of a circle (or of congruent circles) at the centre (corresponding centres) are equal, the chords are equal.

4. The perpendicular from the centre of a circle to a chord bisects the chord.

5. The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.

6. There is one and only one circle passing through three non-collinear points.

7. Equal chords of a circle (or of congruent circles) are equidistant from the centre (or corresponding centres).

8. Chords equidistant from the centre (or corresponding centres) of a circle (or of congruent circles) are equal.

9. If two arcs of a circle are congruent, then their corresponding chords are equal and conversely if two chords of a circle are equal, then their corresponding arcs (minor, major) are congruent.

10. Congruent arcs of a circle subtend equal angles at the centre.

11. The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

12. Angles in the same segment of a circle are equal.

13. Angle in a semicircle is a right angle.

14. If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle.

15. The sum of either pair of opposite angles of a cyclic quadrilateral is 180⁰.

16. If sum of a pair of opposite angles of a quadrilateral is 1800, the quadrilateral is cyclic.

For details of the above learning points join me on my live class in "YouTube" on every Sunday.