Direction Sense - Short-cut Tricks And Examples
Type I: Identify Direction (After Journey)
In this type, based on the conditions given, you have to construct a diagram. Based on your diagram, you have to identify the direction at final spot. Below example will help you to understand better.
Example Question 1: Rahul walks 5 km West, turns southeast and walks 8 km. Again, he turns towards northeast and walks 10 km and then turns to his right. In which direction from his starting point is he standing now?
a) East
b) West
c) Northeast
d) Southeast
Answer: c) Northeast
Reason:
If you apply the conditions given in the question, you will get the below diagram.

From the above diagram, you can say that Rahul is in Northeast direction from his starting point.
Type II: Identify Distance When Start & Finish Points Are in Straight Line
In this type, you will be asked to find the distance between start and finish points. The conditions will be such that the final point will be in straight line with the starting point. Below is an example for this type.
Example Question 2: Sita started from her home towards North and covered a distance of 200 m and then turned to her right and walked 150 m. Then she again turned to her right and walked 75 m and finally she again turned to her right and walked 150 m. How far is she from her home?
a) 125 m
b) 200 m
c) 175 m
d) 150 m
Answer: b) 125 m
Reason:
Based on the question, you will be able to draw the below diagram. As you can see, the starting point A is in straight line with the end point E.
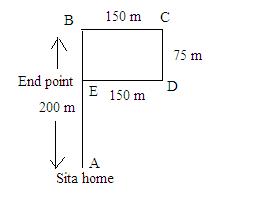
As you know, the above diagram represents the total distance walked by Sita.
Now, we have to find the distance between Sita’s home and the place where she ends i.e., the distance of AE.
Here, AB = 200 m, CD = 75 m
Since CD and BE are parallel lines and BCDE is a rectangle, you can write BE = (CD =) 75 m.
Therefore, you can calculate AE as follows.
AE = AB – BE
= 200 – 75
=125 m.
Type III: Calculate Distance When Start & Finish Points Are NOT in Straight Line
This type is a slight extension of type 2. In this case, the start and finish points will not be in straight line. Below is an example.
Example Question 3: Kishore rides in his bicycle from his home 10 m towards north, then he turns right and travels 15 m, then turns left and travels 10 m and reaches his office. How far is the office from his home?
a) 100 m
b) 25 m
c) 75 m
d) 50 m
Answer: b) 25 m
Reason: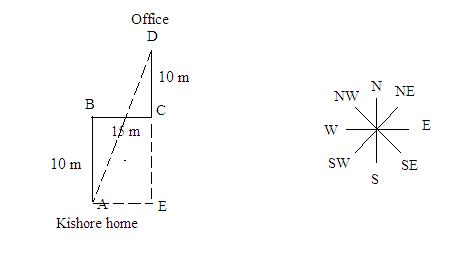
We have to find the distance between Kishore’s home and office.
From the diagram, the distance to find is AD.
From Pythagoras formula,
AD2 = AE2 + ED2 ….. equation 1
But, from the above diagram, ED = EC + CD
ED = 10 + 10 (Because EC = AB = 10 and CD = 10)
= 20
Now you have to substitute the value of ED = 20, in equation 1.
AD2 = 152 + 202
AD2 = 625
AD = 25 m
Type IV: Calculating Direction/Distance When Turns Are Given in Degrees
This type is similar to the above types with one exception. In this case, the turns will be given in degrees. Now let us see an example.
In such problems, whenever you see “clockwise”, you have to understand that the person is turning “right”. Similarly, an “anti-clockwise” turn denotes a “left” turn.
Example Question 4: Gita runs towards north 5 km and from there turned 90˚ anti-clockwise and runs 4 km. Then she takes 135˚ turn clockwise and ran 2 km. Find the direction of Gita with respect to the starting point.
a) South west Region
b) North west Region
c) South east Region
d) North east Region
Answer: d) North east Region
Reason:
You can easily draw the below diagram if you follow the question carefully.
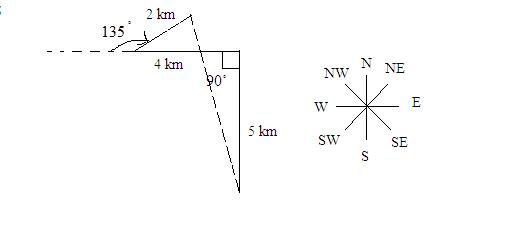
Hence, the final direction is North East.

