न्याय (Syllogism) शार्ट ट्रिक और उदहारण
न्याय, मध्याश्रित अनुमान का वह रूप है, जिसमें दिए गए दो या दो से अधिक कथनों या आधार वाक्यों के आधार पर निष्कर्ष निकाला जाता है। अर्थात दिये गए दो या दो से अधिक कथनों के आधार पर किसी तर्कसंगत निष्कर्ष पर पहुँचना, न्याय कहलाता है।
इस प्रकार की परीक्षा में दो या दो से अधिक आधार वाक्य या कथन (Statement or Premises) दिये गए होते हैं तथा उन पर आधारित दो या दो से अधिक निष्कर्ष (Conclusions) दिये गए होते हैं। आपको इन कथनों को सत्य मानते हुए चाहे वे सर्वज्ञात तथ्यों एवं सर्वमान्य मान्यताओं से सर्वथा परे क्यों न हों, यानी सभी मान्यताओं की अवहेलना करते हुए दिए कथनों के आधार पर तर्कसंगत निष्कर्ष ज्ञात करना होता है।
चूँकि न्याय निगमनात्मक अनुमान है। अतः, निगमन के नियमानुसार निष्कर्ष, कथनों या आधार वाक्यों से अधिक व्यापक नहीं निकाले जाने चाहिए।
कुछ महत्वपूर्ण संकेत
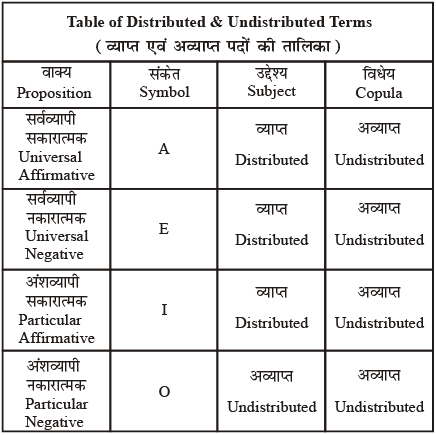
- I. सर्वव्यापी सकारात्मक: इसे तर्क वाक्य में, ‘A’ से निरूपित किया जाता है।
- II. सर्वव्यापी नकारात्मक: इसे तर्क वाक्य में, ‘E’ से निरूपित किया जाता है।
- III. अंशव्यापी सकारात्मक: इसे तर्कवाक्य में, ‘I’ से निरूपित किया जाता है।
- IV. अंशव्यापी नकारात्मक: इसे तर्क वाक्य में ‘O’ से निरूपित किया जाता है।
उदाहरण 1.
कथन I. सभी मनुष्य मरणशील हैं। [A]
कथन II. खुशबू मनुष्य है। [A]
यहाँ हम देख रहे हैं कि दोनों कथनों में ‘मनुष्य’ उभयनिष्ठ हैं। अतः ‘मनुष्य’ मध्य-पद (M) है, जो कि दोनों कथनों के बीच संबंध स्थापित करता है। चूँकि पहले कथन में, मनुष्य तथा मरणशील और दूसरे कथन में खुशबू तथा मनुष्य के बीच संबंध को दर्शाया गया है। अतः निगमन में खुशबू और मरणशील के बीच संबंध स्थापित होगा। अतः वैध निष्कर्ष होगा:
खुशबू मरणशील है। [A]
न्याय के नियमों पर एक दृष्टि
1. दिये गये कथनों में मध्य-पद का होना नितांत आवश्यक है, वर्ना कोई भी वैध निष्कर्ष नहीं निकलेंगे।
उदाहरण 2.
कथन I. सभी कलम दवात हैं। [A]
कथन II. सभी पुस्तक गेंद हैं। [A]
यहाँ हम देख रहे हैं कि उपर्युक्त कथनों में कोई भी मध्य-पद नहीं है, अतः न्याय के नियमानानुसार कोई भी वैध निष्कर्ष नहीं निकलेगा।
उदाहरण 3.
कथन I. सभी कलम दवात हैं। [A]
कथन II. सभी दवात पुस्तक हैं। [A]
निष्कर्ष I. सभी कलम पुस्तक हैं।
निष्कर्ष II. कुछ पुस्तक कलम हैं।
यहाँ हम देख रहे हैं कि दिये गए कथन में मध्य-पद ‘दवात’ पूर्ण समग्रवाची (completely distributed) है। यहाँ निष्कर्ष (I) दिये गये कथनों के आधार पर एक वैध निष्कर्ष है, जबकि निष्कर्ष (II), निष्कर्ष (I) का एक वैध परिवर्तन (conversion) है। अतः निष्कर्ष (I) एवं (II) दोनों तर्कसंगत रूप से निकलते हैं।
2. दिये गए कथनों में मध्य-पद पूर्ण समग्रवाची होना चाहिए वर्ना कोई वैध निष्कर्ष नहीं निकलेंगे।
उदाहरण 4.
कथन I. सभी कुत्ते गधे हैं। [A]
कथन II. सभी गधे घोड़े हैं। [A]
निष्कर्ष I. सभी कुत्ते घोड़े हैं। [A]
निष्कर्ष II. कुछ घोड़े कुत्ते है। [I]
यहाँ हम देख रहे हैं कि मध्य-पद ‘गधे’ पूर्ण समग्रवाची हैं। अतः निष्कर्ष (I) उपर्युक्त कथनों के आधार पर निकाला गया एक वैध निष्कर्ष है, जबकि निष्कर्ष (II), निष्कर्ष (I) का एक वैध परिवर्तन या रूपान्तरण है। अतः निष्कर्ष (I) एवं (II) दोनों तर्कसंगत रूप से निकलते हैं।
उदाहरण 5.
कथन I. सभी लड़के फुटबाॅल हैं। [A]
कथन II. कुछ फुटबाॅल लड़कियाँ हैं। [I]
निष्कर्ष I. सभी लड़के लड़कियाँ हैं। [A]
निष्कर्ष II. कुछ लड़कियाँ लड़के हैं। [I]
यहाँ मध्य-पद ‘फुटबाॅल’ आंशिक समग्रवाची हैं। अतः न्याय के नियमानुसार निष्कर्ष (I) एवं (II) दोनों निष्कर्ष अवैध होंगे।
3. निष्कर्ष में मध्य-पद नहीं आना चाहिए, अन्यथा ऐसे निष्कर्ष को अवैध माना जाएगा।
उदाहरण 6.
कथन I. सभी बाघ बैल हैं। [A]
कथन II. सभी बैल घोड़े हैं। [A]
निष्कर्ष I. सभी बैल बाघ हैं। [A]
निष्कर्ष II. कुछ घोड़े बैल हैं। [I]
यहाँ हम देख रहे हैं कि दोनों निष्कर्ष मे मध्य-पद ‘बैल’ का प्रयोग किया गया है। अतः नियमानुसार दोनों निष्कर्ष अवैध हैं।
4. दिये गए कथनों में से पहला कथन अंशव्यापी सकारात्मक हो एवं दूसरा कथन पूर्णव्यापी सकारात्मक हो तथा मध्य-पद हों तो निष्कर्ष हमेशा अंशव्यापी सकारात्मक में निकलते हैं।
उदाहरण 7.
कथन I. कुछ लड़के पिता हैं। [I]
कथन II. सभी पिता माता हैं। [A]
निष्कर्ष I. कुछ लड़के माता हैं। [I]
निष्कर्ष II. कुछ लड़के माता नहीं हैं। [O]
यहाँ हम देख रहे हैं कि निष्कर्ष (I) उपर्युक्त कथनों का एक वैध निष्कर्ष है। जबकि निष्कर्ष (II) एक अवैध निष्कर्ष है, क्योंकि सकारात्मक कथनों से नकारात्मक निष्कर्ष नहीं निकाले जाते हैं। अतः निष्कर्ष (I) तर्कसंगत रूप से निकलते हैं।
5. दिये गए दोनों कथन अंशव्यापी सकारात्मक हो, तो इन कथनों के आधार पर कोई भी वैध निष्कर्ष नहीं निकलेंगे, क्योंकि अंशव्यापी कथनों में मध्य-पद आंशिक समग्रवाची हो जाते हैं, जबकि निष्कर्ष के लिए न्याय के नियमानुसार मध्य-पद का पूर्ण समग्रवाची होना जरूरी है।
उदाहरण 8.
कथन I. कुछ वृक्ष घोड़े हैं। [I]
कथन II. बिस्कुट एक वृक्ष है। [A]
निष्कर्ष I. बिस्कुट घोड़ा नहीं है। [O]
निष्कर्ष II. कुछ घोड़े वृक्ष हैं। [I]
उपर्युक्त कथन में मध्य-पद ‘वृक्ष’ आंशिक समग्रवाची है अतः न्याय के नियमानुसार इस स्थिति में कोई भी तर्कसंगत वैध निष्कर्ष नहीं निकाले जा सकते हैं। अतः दोनों निष्कर्ष अवैध हैं।
6. दिये गए दोनों कथन पूर्णव्यापी नकारात्मक हो, तो ऐसे कथनों से कोई भी वैध निष्कर्ष नहीं निकाले जा सकते हैं।
उदाहरण 9.
कथन I. कोई लड़की लड़का नहीं हैं। [E]
कथन II. कोई लड़का पिता नहीं हैं। [E]
चूँकि नकारात्मक कथनों में सभी पद व्याप्त हो जाते हैं, अतः ऐसे कथनों से कोई भी तर्कसंगत निष्कर्ष नहीं निकलते हैं।
7. दिये गए कथनों में से यदि पहला कथन पूर्णव्यापी सकारात्मक हो एवं दूसरा कथन पूर्णव्यापी नकारात्मक हो तथा मध्य-पद पूर्ण समग्रवाची हो, तो निष्कर्ष हमेशा पूर्णव्यापी नकारात्मक में निकलते हैं।
उदाहरण 10.
कथन I. सभी नाव जहाज हैं। [A]
कथन II. कोई भी जहाज मछली नहीं हैं। [E]
निष्कर्ष I. सभी जहाज नाव हैं। [A]
निष्कर्ष II. कोई भी नाव मछली नहीं है। [E]
यहाँ नियमानुसार सकारात्मक निष्कर्ष नहीं निकलने चाहिए, अतः निष्कर्ष (I) एक अवैध निष्कर्ष है। जबकि निष्कर्ष (II) उपर्युक्त कथनों के आधार पर निकाला गया एक वैध निष्कर्ष है। अतः निष्कर्ष (II) तर्कसंगत रूप से निकलता है।
8. यदि पहला कथन अंशव्यापी सकारात्मक हो तथा दूसरा कथन पूर्णव्यापी नकारात्मक हो एवं मध्य-पद व्याप्त हो, तो निष्कर्ष हमेशा अंशव्यापी नकारात्मक में निकलते हैं।
उदाहरण 11.
कथन I. कुछ बाघ हाथी हैं। [I]
कथन II. कोई हाथी कुत्ता नहीं है। [E]
निष्कर्ष I. कुछ बाघ कुत्ता नहीं है। [O]
निष्कर्ष II. कुछ कुत्ता बाघ नहीं है। [O]
यहाँ निष्कर्ष (I) उपर्युक्त कथन का एक वैध निष्कर्ष है, जबकि निष्कर्ष (II), निष्कर्ष (I) का एक वैध रूपान्तरण या परिवर्तन है। अतः दोनों निष्कर्ष तर्कसंगत रूप से निकलते हैं।
9. दिये गए कथनों में से यदि पहला कथन पूर्णव्यापी नकारात्मक हो एवं दूसरा कथन पूर्णव्यापी सकारात्मक हो, तो निष्कर्ष अंशव्यापी नकारात्मक में निकले जा सकते हैं।
उदाहरण 12.
कथन I. कोई भी कवि कलाकार नहीं हैं। [E]
कथन II. सभी कलाकार निर्धन हैं। [A]
निष्कर्षः कोई भी कवि निर्धन नहीं है। [E]
यहाँ कथन (I) पूर्णव्यापी नकारात्मक है एवं कथन (II) पूर्णव्यापी सकारात्मक है, अतः निष्कर्ष अवैध है।
10. दिये गए कथन में यदि पहला कथन पूर्णव्यापी नकारात्मक हो एवं दूसरा कथन अंशव्यापी सकारात्मक हो, तो निष्कर्ष हमेशा अंशव्यापी नकारात्मक में निकलते हैं।
उदाहरण 13.
कथन I. कोई भी गायक कलाकार नहीं है। [E]
कथन II. कुछ कलाकार निर्माता हैं। [I]
निष्कर्ष I. कोई भी गायक निर्माता नहीं है। [E]
निष्कर्ष II. कुछ निर्माता गायक नहीं हैं। [O]
यहाँ हम देख रहे हैं कि निष्कर्ष (I) में पद ‘निर्माता’ को व्याप्त कर दिया गया है जोकि कथन में अव्याप्त था। अतः निष्कर्ष (I) अवैध है जबकि (II) वैध है।
11. यदि मध्य-पद द्विअर्थी (ambiguous) हो तो कोई भी वैध निष्कर्ष नहीं निकलते हैं।
उदाहरण 14.
कथन I. सभी फूल खुशबू देते हैं। [A]
कथन II. खुशबू आर्या की बहन है। [A]
निष्कर्ष I. सभी फूल आर्या की बहन हैं। [A]
निष्कर्ष II. कुछ आर्या की बहन फूल हैं। [I]
यहाँ हम देख रहे हैं कि दोनों कथनों में प्रयुक्त पद खुशबू एक जैसे प्रतीत होते हैं लेकिन अर्थ की दृष्टिकोण से दोनों का अलग-अलग अर्थ निकलता है, क्योंकि कथन (I) में ‘खुशबू’ भाव को व्यक्त करता है, जबकि (II) कथन में ‘खुशबू’ नाम को व्यक्त कर रहा है। अतः मध्य-पद द्विअर्थी हैं, अतः निष्कर्ष (I) एवं (II) दोनों अवैध हैं।
न्याय के अपवाद नियम (Exceptional Rules)
1. यदि पहला कथन अंशव्यापी सकारात्मक हो तथा दूसरा कथन पूर्णव्यापी सकारात्मक हो लेकिन ‘मध्य-पद’ अव्याप्त हो, तो इन कथनों के आधार पर संभावित निष्कर्ष निकाले जा सकते हैं। ऐसे निष्कर्ष एक साथ सत्य नहीं होते हैं लेकिन एक साथ दोनों असत्य हो सकते हैं। इसे विपरीत निष्कर्ष भी कह सकते हैं।
उदाहरण 15.
कथन I. कुछ डाॅक्टर मूर्ख हैं। [I]
कथन II. आर्या एक डाॅक्टर है। [A]
निष्कर्ष I. कुछ मूर्ख डाॅक्टर हैं। [I]
निष्कर्ष II. आर्या मूर्ख है। [A]
चूंँकि दिये गए कथनों में ‘मध्य-पद’ आंशिक समग्रवाची हैं साथ ही निष्कर्ष पूरक (complementary) नहीं है, अतः कोई वैध निष्कर्ष नहीं निकाला जा सकता है। अतः निष्कर्ष (I) एवं (II) दोनों अवैध हैं।
उदाहरण 16.
कथन I. कुछ डाॅक्टर विद्वान हैं। [I]
कथन II. आर्या एक डाॅक्टर है। [A]
निष्कर्ष I. आर्या विद्वान हो सकते हैं। [A]
निष्कर्ष II. आर्या विद्वान नहीं हो सकते हैं। [E]
ऐसे निष्कर्ष संभावित होते हैं। अतः या तो निष्कर्ष (I) या तो निष्कर्ष (II) को तर्कसंगत संभावित निष्कर्ष माना जा सकता है।
2. यदि दिये गए कथन अंशव्यापी सकारात्मक हो तथा किसी एक कथन में लिंग को दर्शाया गया हो, तो निष्कर्ष संभावनापूर्ण निकलते हैं।
उदाहरण 17.
कथन I. कुछ अधिवक्ता महिला हैं। [I]
कथन II. आर्या एक अधिवक्ता है। [A]
निष्कर्ष I. आर्या एक महिला अधिवक्ता है। [A]
निष्कर्ष II. आर्या एक पुरुष अधिवक्ता है। [A]
उपर्युक्त दोनों निष्कर्षों में से या तो (I) या (II) निष्कर्ष को संभावित निष्कर्ष के रूप में माना जा सकता है। न्याय में ‘नाम’ के आधार पर लिंग को निरूपित करना अवैध होता है। यानी आर्या ‘महिला’ भी हो सकती है या ‘पुरुष‘ भी हो सकती है।
अतः या तो निष्कर्ष (I) या तो निष्कर्ष (II) तर्कसंगत रूप से निकलते हैं।
3. यदि पहला कथन पूर्णव्यापी सकारात्मक (Universal Affirmative) तथा दूसरा कथन पूर्णव्यापी नकारात्मक (Universal Negative) निम्न प्रकार से हों, तो पूर्णव्यापी नकारात्मक में निष्कर्ष निकाले जा सकते हैं।
उदाहरण 18.
कथन I. सभी लड़कियाँ सुन्दर हैं। [A]
कथन II. कोई भी लड़का सुंदर नहीं है। [E]
निष्कर्ष I. कोई भी लड़का, लड़की नहीं है। [E]
निष्कर्ष II. कोई भी लड़की, लड़का नहीं है। [E]
व्याख्याः यहाँ निष्कर्ष (I) तथा निष्कर्ष (II), मध्याश्रित एवं साक्षात् अनुमान के नियमानुसार दोनों वैध निष्कर्ष हैं।
स्मरणीय तथ्य (Points to Remember)
निम्नलिखित 6 परिस्थितियों में कोई भी निष्कर्ष स्थापित किया जा सकता है। अन्य सभी परिस्थितियों में कोई निष्कर्ष स्थापित नहीं किया जा सकता।
यदि दो कथनों में कोई उभयनिष्ठ पद नहीं हो तब उससे कोई निष्कर्ष नहीं निकाला जा सकता।
साधित उदाहरण (Solved Examples)
1. कथन:
I. कुछ कार रोड हैं।
II. कुछ रोड बस हैं।
हलः निष्कर्ष:कुछ कार रोड हैं। (I-type)
कुछ रोड बस हैं। (I-type)
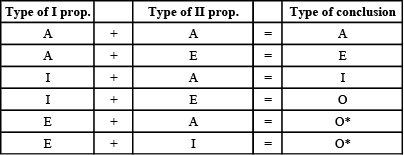
निष्कर्ष: I + I = कोई निष्कर्ष नहीं
चूंकि दोनों कथन (I-type) के हैं अतः कोई बीच का निष्कर्ष (mediate conclusions) नहीं निकलता है लेकिन तुरन्त बाद का (immediate conclusions) निष्कर्ष कथन (I) और (II) के व्युत्क्रम (conversion) से निकल सकता है।
निष्कर्ष (i) कुछ रोड कार हैं। (कथन I का व्युत्क्रम)
निष्कर्ष (ii) कुछ बस रोड हैं। (कथन II का व्युत्क्रम)
2. कथन:
I. कुछ मनुष्य शेर हैं।
II. सभी शेर लोमड़ी हैं।
हलः निष्कर्ष: कुछ मनुष्य शेर हैं।(I-type)
सभी शेर लोमड़ी हैं। (A-type)
निष्कर्ष (i) कुछ मनुष्य लोमड़ी हैं (I + A = I-type)
निष्कर्ष (ii) कुछ शेर मनुष्य हैं। (कथन I का व्युत्क्रम)
निष्कर्ष (iii) कुछ लोमड़ी शेर हैं। (कथन II का व्युत्क्रम)
3. कथन:
I. सभी पक्षी किताबें हैं।
II. सभी किताबें कार हैं।
हलः निष्कर्ष: सभी पक्षी किताबे हैं (A-type)
सभी किताबें कार हैं (A-type)
निष्कर्ष (i) सभी पक्षी कार हैं। (A + A = A-type)
निष्कर्ष (ii) कुछ पक्षी कार हैं। (Implication of I)
निष्कर्ष (iii) कुछ किताबें कार हैं। (Implication of II)
निष्कर्ष (iv) कुछ किताबें पक्षी हैं। (कथन I का व्युत्क्रम)
निष्कर्ष (v) कुछ कार किताबें हैं। (कथन II का व्युत्क्रम)
4. कथन:
I. कुछ कुत्ते बिल्लियाँ हैं।
II. कोई बिल्ली गाय नहीं है।
हलः निष्कर्ष (i) कुछ कुत्ते गाय नहीं हैं। (I + E = O-type)
निष्कर्ष (ii) कुछ बिल्लियाँ कुत्ते हैं। (कथन I का व्युत्क्रम)
निष्कर्ष (iii) कुछ बिल्लियाँ गाय नहीं हैं। (Implication of II)
निष्कर्ष (iv) कुछ गाय ‘बिल्ली’ हैं। (कथन II का व्युत्क्रम)
5. कथन:
I. सभी पिता बेटे हैं
II. कोई बेटा एडुकेटेड नहीं है।
हलः निष्कर्ष:सभी पिता बेटे हैं। (A-type)
कोई बेटा एडुकेटेड नहीं है। (E-type)
निष्कर्ष (i) कोई पिता एडुकेटेड नहीं हैं। (A + E = E-type)
निष्कर्ष (ii) कुछ पिता बेटे हैं। (Implication of I)
निष्कर्ष (iii) कुछ बेटे पिता हैं। (कथन I का व्युत्क्रम)
निष्कर्ष (iv) कुछ बेटे एडुकेटेड नहीं हैं। (Implication of II)
6. कथन:
I. कोई मैगजीन टोपी नहीं है।
II. सभी टोपी कैमरा हैं।
हलः निष्कर्ष: कोई मैगजीन टोपी नहीं है।
सभी टोपी कैमरा हैं।
निष्कर्ष (i) कुछ कैमरा मैगजीन नहीं हैं। (E + A = O*-type)
निष्कर्ष (ii) कुछ टोपी कैमरा हैं। (Implication of II)
निष्कर्ष (iii) कुछ मैगजीन टोपी नहीं हैं। (Implication of I)
निष्कर्ष (iv) कुछ कैमरा टोपी हैं। (कथन II का व्युत्क्रम)
निष्कर्ष (v) कोई टोपी मैगजीन नहीं है। (कथन I का व्युत्क्रम)
7. कथन:
I. कोई टेबल पानी नहीं है।
II. कुछ पानी कपड़े हैं।
हलः निष्कर्ष:कोई टेबल पानी नहीं है।
कुछ पानी कपड़े हैं।
निष्कर्ष (i) कुछ कपड़े टेबल नहीं है। (E + A = O*-type)
निष्कर्ष (ii) कुछ टेबल पानी नहीं हैं। (Implication of I)
निष्कर्ष (iii) कोई पानी टेबल नहीं है। (कथन I का व्युत्क्रम)
निष्कर्ष (iv) कुछ कपड़े पानी हैं। (कथन II का व्युत्क्रम)
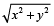 होती है।
होती है।