Measurement of Length
You are already familiar with some direct methods for the measurement of length. For example, a metre scale is used for lengths from 10–3 m to 102 m. A vernier callipers is used for lengths to an accuracy of 10–4 m. A screw gauge and a spherometer can be used to measure lengths as less as to 10–5 m. To measure lengths beyond these ranges, we make use of some special indirect methods.
Measurement of Large Distances
Large distances such as the distance of a planet or a star from the earth cannot be measured directly with a metre scale. An important method in such cases is the parallax method.
When you hold a pencil in front of you against some specific point on the background (a wall) and look at the pencil first through your left eye A (closing the right eye) and then look at the pencil through your right eye B (closing the left eye), you would notice that the position of the pencil seems to change with respect to the point on the wall. This is called parallax. The distance between the two points of observation is called the basis. In this example, the basis is the distance between the eyes.
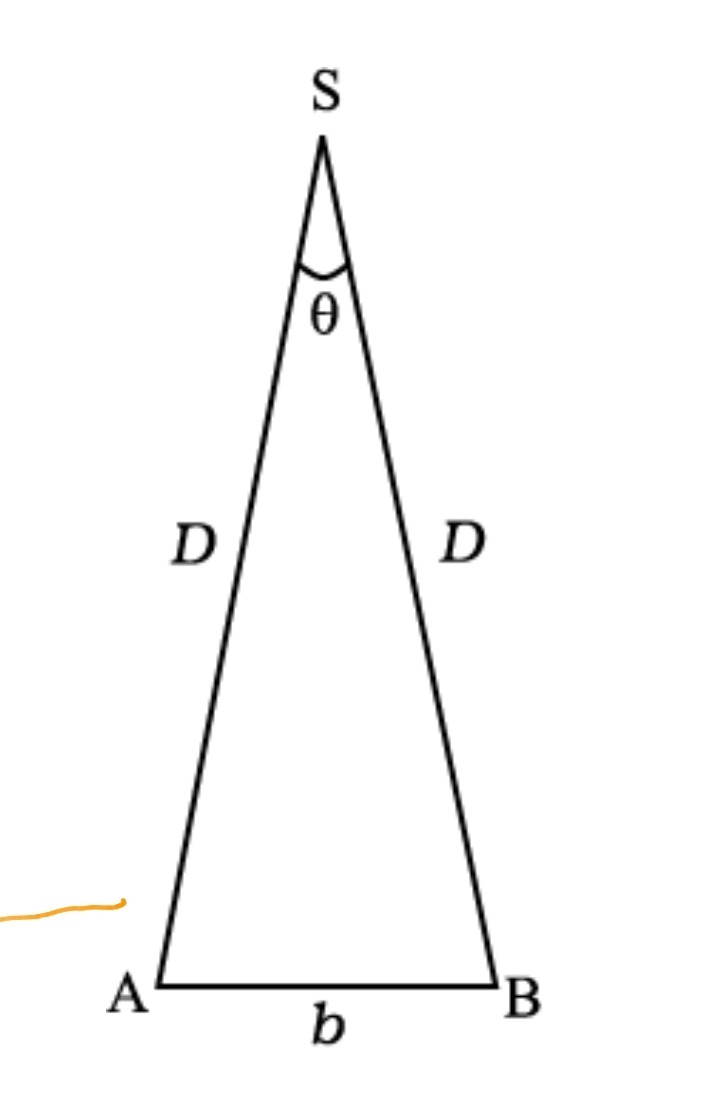
To measure the distance D of a far away planet S by the parallax method, we observe it from two different positions (observatories) A and B on the Earth, separated by distance AB = b at the same time as shown in Fig. 2.2. We measure the angle between the two directions along which the planet is viewed at these two points. The ∠ASB in Fig. 2.2 represented by symbol θ is called the parallax angle or parallactic angle.
As the planet is very far away,
b/D <<1
and therefore,
D = b/θ
is very small. Then we approximately take AB as an arc of length b of a circle with centre at S and the distance D as the radius AS = BS so that AB = b = D θ where θ is in radians.
(2.1)
Having determined D, we can employ a similar method to determine the size or angular diameter of the planet. If d is the diameter of the planet and α the angular size of the planet (the angle subtended by d at the earth), we have
α = d/D (2.2)
Fig. 2.2 Parallax method.
The angle α can be measured from the same location on the earth. It is the angle between the two directions when two diametrically opposite points of the planet are viewed through the telescope. Since D is known, the diameter d of the planet can be determined using Eq. (2.2).
Estimation of Very Small Distances: Size of a Molecule
To measure a very small size, like that of a molecule (10–8 m to 10–10 m), we have to adopt special methods. We cannot use a screw gauge or similar instruments. Even a microscope has certain limitations. An optical microscope uses visible light to ‘look’ at the system under investigation. As light has wave like features, the resolution to which an optical microscope can be used is the wavelength of light (A detailed explanation can be found in the Class XII Physics textbook). For visible light the range of wavelengths is from about 4000 Å to 7000 Å
(1 angstrom = 1 Å = 10-10 m). Hence an optical microscope cannot resolve particles with sizes smaller than this. Instead of visible light, we can use an electron beam. Electron beams can be focussed by properly designed electric and magnetic fields. The resolution of such an electron microscope is limited finally by the fact that electrons can also behave as waves . The wavelength of an electron can be as small as a fraction of an angstrom. Such electron microscopes with a resolution of 0.6 Å have been built. They can almost resolve atoms and molecules in a material. In recent times, tunnelling microscopy has been developed in which again the limit of resolution is better than an angstrom. It is possible to estimate the sizes of molecules.
A simple method for estimating the molecular size of oleic acid is given below. Oleic acid is a soapy liquid with large molecular size of the order of 10–9 m.
The idea is to first form mono-molecular layer of oleic acid on water surface.
We dissolve 1 cm3 of oleic acid in alcohol to make a solution of 20 cm3. Then we take 1 cm3 of this solution and dilute it to 20 cm3, using alcohol. So, the concentration of the solution is equal to
(1/20×20) cm³
of oleic acid/cm3 of solution. Next we lightly sprinkle some lycopodium powder on the surface of water in a large trough and we put one drop of this solution in the water. The oleic acid drop spreads into a thin, large and roughly circular film of molecular thickness on water surface. Then, we quickly measure the diameter of the thin film to get its area A. Suppose we have dropped n drops in the water. Initially, we determine the approximate volume of each drop (V cm3).
Volume of n drops of solution
= nV cm3
Amount of oleic acid in this solution
=
nV(1/20×20) cm³
This solution of oleic acid spreads very fast on the surface of water and forms a very thin layer of thickness t. If this spreads to form a film of area A cm2, then the thickness of the film
t = Volume of the film /Area of the film
or,
t = nV(1/20×20A) cm
(2.3)
If we assume that the film has mono-molecular thickness, then this becomes the size or diameter of a molecule of oleic acid. The value of this thickness comes out to be of the order of 10–9 m.