The International System of Units
In earlier time scientists of different countries were using different systems of units for measurement. Three such systems, the CGS, the FPS (or British) system and the MKS system were in use extensively till recently.
The base units for length, mass and time in these systems were as follows :
• In CGS system they were centimetre, gram and second respectively.
• In FPS system they were foot, pound and second respectively.
• In MKS system they were metre, kilogram and second respectively.
The system of units which is at present internationally accepted for measurement is the Système Internationale
d’ Unites (French for International System of Units), abbreviated as SI. The SI, with standard scheme of symbols, units and abbreviations, developed by the Bureau International des Poids et measures (The International Bureau of weights and measures, BIPM) in 1971 were recently revised by the General Conference on weights and measures in November 2018. The scheme is now for international usage in scientific, technical, industrial and commercial work. Because SI units used decimal system, conversions within the system are quite simple and convenient. We shall follow the SI units in this book.
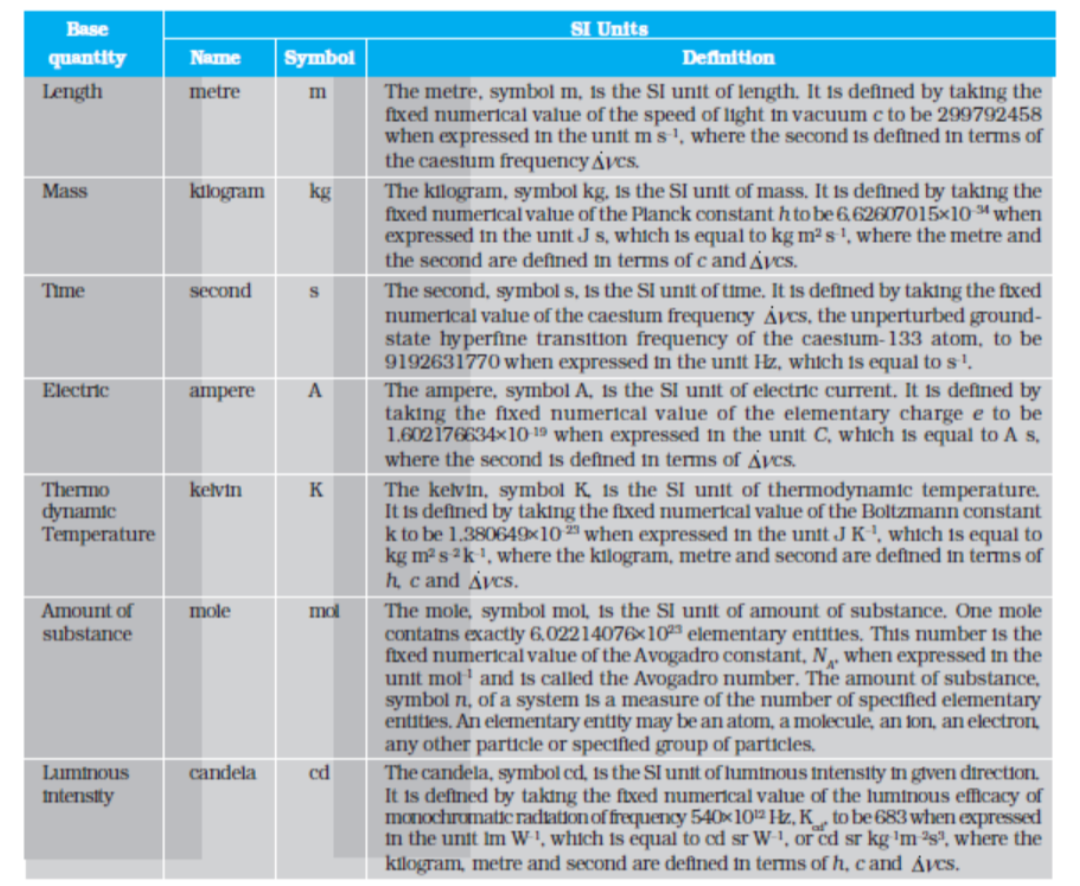
In SI, there are seven base units as given in Table 2.1. Besides the seven base units, there are two more units that are defined for (a) plane angle dθ as the ratio of length of arc ds to the radius r and (b) solid angle dΩ as the ratio of the intercepted area dA of the spherical surface, described about the apex O as the centre, to the square of its radius r, as shown in Fig. 2.1(a) and (b) respectively. The unit for plane angle is radian with the symbol rad and the unit for the solid angle is steradian with the symbol sr. Both these are dimensionless quantities.
Fig. 2.1 Description of (a) plane angle dθ and (b) solid angle
Table 2.1 SI Base Quantities and Units*
* The values mentioned here need not be remembered or asked in a test. They are given here only to indicate the extent of accuracy to which they are measured. With progress in technology, the measuring techniques get improved leading to measurements with greater precision. The definitions of base units are revised to keep up with this progress.
Table 2.2 Some units retained for general use (Though outside SI)
Note that when mole is used, the elementary entities must be specified. These entities may be atoms, molecules, ions, electrons, other particles or specified groups of such particles.
We employ units for some physical quantities that can be derived from the seven base units (Appendix A 6). Some derived units in terms of the SI base units are given in (Appendix A 6.1). Some SI derived units are given special names (Appendix A 6.2 ) and some derived SI units make use of these units with special names and the seven base units (Appendix A 6.3). These are given in Appendix A 6.2 and A 6.3 for your ready reference. Other units retained for general use are given in Table 2.2.
Common SI prefixes and symbols for multiples and sub-multiples are given in Appendix A2. General guidelines for using symbols for physical quantities, chemical elements and nuclides are given in Appendix A7 and those for SI units and some other units are given in Appendix A8 for your guidance and ready reference.